Giải Toán 11 trang 123 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 123 Tập 1 trong Bài tập cuối Chương 5 Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 123.

Giải Toán 11 trang 123 Tập 1 Kết nối tri thức

Bài 5.18 trang 123 Toán 11 Tập 1: Cho dãy số (u_n) với $u_n=\sqrt{n^2+1}-\sqrt{n}$. Mệnh đề đúng là

A. $\underset{n\to +\infty }{\lim }{u}_n=-\infty$.

B. $\underset{n\to +\infty }{\lim }{u}_n=1$.

C. $\underset{n\to +\infty }{\lim }{u}_n=+\infty$.

D. $\underset{n\to +\infty }{\lim }{u}_n=0$.

Lời giải:

Đáp án đúng là: C

Ta có: $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\left(\sqrt{n^2+1}-\sqrt{n}\right)$$=\underset{n\to +\infty }{\lim }\left(\sqrt{n^2\left(1+\frac{1}{n^2}\right)}-\sqrt{n}\right)$

Vì $\underset{n\to +\infty }{\lim }n=+\infty$ và $\underset{n\to +\infty }{\lim }\left(\sqrt{1+\frac{1}{n^2}}-\frac{1}{\sqrt{n}}\right)=1>0$.

Do đó Vậy $\underset{n\to +\infty }{\lim }{u}_n=+\infty$.

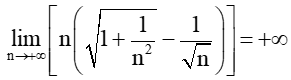
Bài 5.19 trang 123 Toán 11 Tập 1: Cho $u_n=\frac{2+2^2+\mathrm{...}+2^n}{2^n}$. Giới hạn của dãy số (u_n) bằng

A. 1.

B. 2.

C. – 1.

D. 0.

Lời giải:

Đáp án đúng là: B

Ta có: 2 + 2² + ... + 2ⁿ, đây là tổng của n số hạng đầu của cấp số nhân với số hạng đầu là u₁ = 2 và công bội q = 2. Do đó, 2 + 2² + ... + 2ⁿ = $\frac{u_1\left(1-q^n\right)}{1-q}=\frac{2\left(1-2^n\right)}{1-2}=-2\left(1-2^n\right)$.

Khi đó, $u_n=\frac{2+2^2+\mathrm{...}+2^n}{2^n}$$=\frac{-2\left(1-2^n\right)}{2^n}$$=\frac{2^n-1}{2^{n-1}}=2-\frac{1}{2^{n-1}}$.

Vậy $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\left(2-\frac{1}{2^{n-1}}\right)=2$.

Bài 5.20 trang 123 Toán 11 Tập 1: Cho cấp số nhân lùi vô hạn (u_n) với $u_n=\frac{2}{3^n}.$ Tổng của cấp số nhân này bằng

A. 3.

B. 2.

C. 1.

D. 6.

Lời giải:

Đáp án đúng là: C

Ta có: $u_1=\frac{2}{3^1}=\frac{2}{3}$, $u_2=\frac{2}{3^2}=\frac{2}{9}$, do đó công bội của cấp số nhân là $q=\frac{u_2}{u_1}=\frac{2}{9}:\frac{2}{3}=\frac{1}{3}$.

Khi đó, tổng của cấp số nhân lùi vô hạn đã cho là $S=\frac{u_1}{1-q}=\frac{\frac{2}{3}}{1-\frac{1}{3}}=1$.

Bài 5.21 trang 123 Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\sqrt{x+1}-\sqrt{x+2}$. Mệnh đề đúng là

A. $\underset{x\to +\infty }{\lim }f\left(x\right)=-\infty$.

B. $\underset{x\to +\infty }{\lim }f\left(x\right)=0$.

C. $\underset{x\to +\infty }{\lim }f\left(x\right)=-1$.

D. $\underset{x\to +\infty }{\lim }f\left(x\right)=-\frac{1}{2}$.

Lời giải:

Đáp án đúng là: B

Ta có: $f\left(x\right)=\sqrt{x+1}-\sqrt{x+2}$$=\frac{{\left(\sqrt{x+1}\right)}^2-{\left(\sqrt{x+2}\right)}^2}{\sqrt{x+1}+\sqrt{x+2}}$

$=\frac{\left(x+1\right)-\left(x+2\right)}{\sqrt{x+1}+\sqrt{x+2}}$$=\frac{-1}{\sqrt{x+1}+\sqrt{x+2}}$.

Do đó, $\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{-1}{\sqrt{x+1}+\sqrt{x+2}}$= 0.

Bài 5.22 trang 123 Toán 11 Tập 1: Cho hàm số 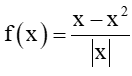. Khi đó $\underset{x\to 0^{+}}{\lim }f\left(x\right)$ bằng

A. 0.

B. 1.

C. +∞.

D. – 1.

Lời giải:

Đáp án đúng là: B

Ta có: .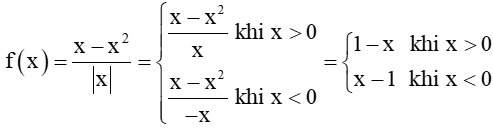

Do đó, $\underset{x\to 0^{+}}{\lim }f\left(x\right)$$=\underset{x\to 0^{+}}{\lim }\left(1-x\right)=1-0=1$.

Bài 5.23 trang 123 Toán 11 Tập 1: Cho hàm số . Hàm số f(x) liên tục trên

A. (–∞; +∞).

B. (–∞; – 1].

C. (–∞; – 1) ∪ (– 1; +∞).

D. [– 1; +∞).

Lời giải:

Đáp án đúng là: C

Ta có: .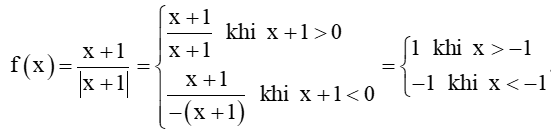

Tập xác định của hàm số là D = (–∞; – 1) ∪ (– 1; +∞).

Từ đó suy ra hàm số đã cho liên tục trên (–∞; – 1) ∪ (– 1; +∞).

Bài 5.24 trang 123 Toán 11 Tập 1: Cho hàm số Hàm số 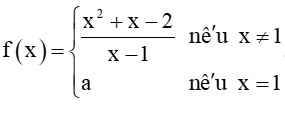liên tục tại x = 1 khi

A. a = 0.

B. a = 3.

C. a = – 1.

D. a = 1.

Lời giải:

Đáp án đúng là: B

Ta có: $\underset{x\to 1}{\lim }f\left(x\right)=\underset{x\to 1}{\lim }\frac{x^2+x-2}{x-1}$$=\underset{x\to 1}{\lim }\frac{\left(x-1\right)\left(x+2\right)}{x-1}$$=\underset{x\to 1}{\lim }\left(x+2\right)=1+2=3$.

f(1) = a.

Để hàm số f(x) liên tục tại x = 1 thì $\underset{x\to 1}{\lim }f\left(x\right)=f\left(1\right)$⇔ a = 3.

Lời giải bài tập Toán 11 Bài tập cuối Chương 5 Kết nối tri thức hay khác:

• Giải Toán 11 trang 124