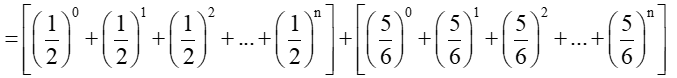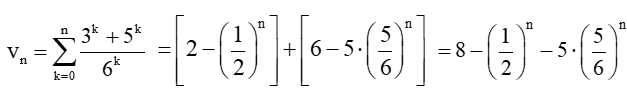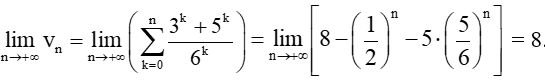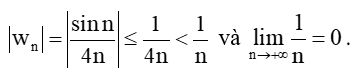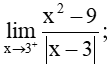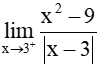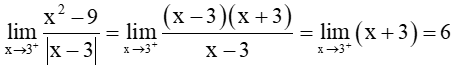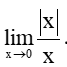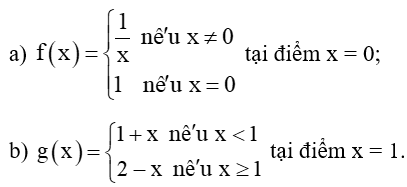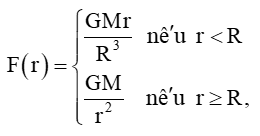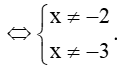Giải Toán 11 trang 124 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 124 Tập 1 trong Bài tập cuối Chương 5 Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 124.

Giải Toán 11 trang 124 Tập 1 Kết nối tri thức

Bài 5.25 trang 124 Toán 11 Tập 1: Cho dãy số (u_n) có tính chất 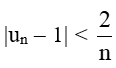. Có kết luận gì về giới hạn của dãy số này?

Lời giải:

Vì

Do đó, $\underset{n\to +\infty }{\lim }\left(u_n-1\right)=0$. Từ đó suy ra $\underset{n\to +\infty }{\lim }{u}_n=1$.

Bài 5.26 trang 124 Toán 11 Tập 1: Tìm giới hạn của các dãy số sau:

a) $u_n=\frac{n^2}{3n^2+7n-2}$;

b) $v_n=\sum _{k=0}^n\frac{3^k+5^k}{6^k}$;

c) ${\text{w}}_n=\frac{\sin n}{4n}$.

Lời giải:

a) $u_n=\frac{n^2}{3n^2+7n-2}$

Ta có: $\underset{n\to +\infty }{\lim }{u}_n=\underset{n\to +\infty }{\lim }\frac{n^2}{3n^2+7n-2}$$=\underset{n\to +\infty }{\lim }\frac{n^2}{n^2\left(3+\frac{7}{n}-\frac{2}{n^2}\right)}$$=\underset{n\to +\infty }{\lim }\frac{1}{3+\frac{7}{n}-\frac{2}{n^2}}=\frac{1}{3}$

b) $v_n=\sum _{k=0}^n\frac{3^k+5^k}{6^k}$$=\frac{3^0+5^0}{6^0}+\frac{3^1+5^1}{6^1}+\frac{3^2+5^2}{6^2}+\mathrm{...}+\frac{3^n+5^n}{6^n}$

$=\left(\frac{3^0}{6^0}+\frac{5^0}{6^0}\right)+\left(\frac{3^1}{6^1}+\frac{5^1}{6^1}\right)+\left(\frac{3^2}{6^2}+\frac{5^2}{6^2}\right)+\mathrm{...}+\left(\frac{3^n}{6^n}+\frac{5^n}{6^n}\right)$

$=\left({\left(\frac{1}{2}\right)}^0+{\left(\frac{5}{6}\right)}^0\right)+\left({\left(\frac{1}{2}\right)}^1+{\left(\frac{5}{6}\right)}^1\right)+\left({\left(\frac{1}{2}\right)}^2+{\left(\frac{5}{6}\right)}^2\right)+\mathrm{...}+\left({\left(\frac{1}{2}\right)}^n+{\left(\frac{5}{6}\right)}^n\right)$

Vì ${\left(\frac{1}{2}\right)}^1+{\left(\frac{1}{2}\right)}^2+\mathrm{...}+{\left(\frac{1}{2}\right)}^n$ là tổng n số hạng đầu của cấp số nhân với số hạng đầu là ${\left(\frac{1}{2}\right)}^1=\frac{1}{2}$ và công bội là $\frac{1}{2}$ nên

${\left(\frac{1}{2}\right)}^0+{\left(\frac{1}{2}\right)}^1+{\left(\frac{1}{2}\right)}^2+\mathrm{...}+{\left(\frac{1}{2}\right)}^n={\left(\frac{1}{2}\right)}^0+\frac{\frac{1}{2}\left(1-{\left(\frac{1}{2}\right)}^n\right)}{1-\frac{1}{2}}$$=1+\left(1-{\left(\frac{1}{2}\right)}^n\right)=2-{\left(\frac{1}{2}\right)}^n$.

Tương tự, ta tính được:

${\left(\frac{5}{6}\right)}^0+{\left(\frac{5}{6}\right)}^1+{\left(\frac{5}{6}\right)}^2+\mathrm{...}+{\left(\frac{5}{6}\right)}^n={\left(\frac{5}{6}\right)}^0+\frac{\frac{5}{6}\left(1-{\left(\frac{5}{6}\right)}^n\right)}{1-\frac{5}{6}}$$=1+5\left(1-{\left(\frac{5}{6}\right)}^n\right)=6-5\cdot {\left(\frac{5}{6}\right)}^n$.

Do đó,

Vậy

c) ${\text{w}}_n=\frac{\sin n}{4n}$

Ta có:

Do đó, $\underset{n\to +\infty }{\lim }{\text{w}}_n=\underset{n\to +\infty }{\lim }\frac{\sin n}{4n}=0$.

Bài 5.27 trang 124 Toán 11 Tập 1: Viết các số thập phân vô hạn tuần hoàn sau đây dưới dạng phân số.

a) 1,(01);

b) 5,(132).

Lời giải:

a) Ta có: 1,(01) = 1,010101... = 1 + 0,01 + 0,0001 + 0,000001 + ...

= 10⁰ + 10^-2 + 10^-4 + 10^-6 + ...

Đây là tổng của cấp số nhân lùi vô hạn với u₁ = 10⁰ = 1 và q = 10^-2 nên

1,(01) = $\frac{u_1}{1-q}=\frac{1}{1-{10}^{-2}}=\frac{100}{99}$.

b) Ta có: 5,(132) = 5,132132132... = 5 + 0,132 + 0,000132 + 0,000000132 + ...

= 5 + 0,132 + 0,132 . 10^-3 + 0,132 . 10^-6 + ...

Vì 0,132 + 0,132 . 10^-3 + 0,132 . 10^-6 + ... là tổng của cấp số nhân lùi vô hạn với u₁ = 0,132 và q = 10^-3 nên

0,132 + 0,132 . 10^-3 + 0,132 . 10^-6 + ... = $\frac{u_1}{1-q}=\frac{0,132}{1-{10}^{-3}}=\frac{44}{333}$.

Do đó 5,(132) = 5 + $\frac{44}{333}$ = $\frac{1709}{333}$.

Bài 5.28 trang 124 Toán 11 Tập 1: Tính các giới hạn sau:

a) $\underset{x\to 7}{\lim }\frac{\sqrt{x+2}-3}{x-7}$;

b) $\underset{x\to 1}{\lim }\frac{x^3-1}{x^2-1}$;

c) $\underset{x\to 1}{\lim }\frac{2-x}{{\left(1-x\right)}^2}$;

d) $\underset{x\to -\infty }{\lim }\frac{x+2}{\sqrt{4x^2+1}}$.

Lời giải:

a) $\underset{x\to 7}{\lim }\frac{\sqrt{x+2}-3}{x-7}$$=\underset{x\to 7}{\lim }\frac{{\left(\sqrt{x+2}\right)}^2-3^2}{\left(x-7\right)\left(\sqrt{x+2}+3\right)}$

$=\underset{x\to 7}{\lim }\frac{x-7}{\left(x-7\right)\left(\sqrt{x+2}+3\right)}$$=\underset{x\to 7}{\lim }\frac{1}{\sqrt{x+2}+3}$$=\frac{1}{\sqrt{7+2}+3}=\frac{1}{6}$.

b) $\underset{x\to 1}{\lim }\frac{x^3-1}{x^2-1}$$=\underset{x\to 1}{\lim }\frac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}$$=\underset{x\to 1}{\lim }\frac{x^2+x+1}{x+1}=\frac{1^2+1+1}{1+1}=\frac{3}{2}$.

c) $\underset{x\to 1}{\lim }\frac{2-x}{{\left(1-x\right)}^2}$

Ta có: $\underset{x\to 1}{\lim }\left(2-x\right)=2-1=1>0$;

$\underset{x\to 1}{\lim }{\left(1-x\right)}^2=0$ và (1 – x)² > 0 với mọi x ≠ 1.

Do vậy, $\underset{x\to 1}{\lim }\frac{2-x}{{\left(1-x\right)}^2}=+\infty$.

d) $\underset{x\to -\infty }{\lim }\frac{x+2}{\sqrt{4x^2+1}}$$=\underset{x\to -\infty }{\lim }\frac{x+2}{\sqrt{x^2\left(4+\frac{1}{x^2}\right)}}$

$=\underset{x\to -\infty }{\lim }\frac{x\left(1+\frac{2}{x}\right)}{-x\sqrt{4+\frac{1}{x^2}}}$$=\underset{x\to -\infty }{\lim }\frac{-\left(1+\frac{2}{x}\right)}{\sqrt{4+\frac{1}{x^2}}}$$=-\frac{1}{2}$.

Bài 5.29 trang 124 Toán 11 Tập 1: Tính các giới hạn một bên:

a)

b) $\underset{x\to 1^{-}}{\lim }\frac{x}{\sqrt{1-x}}$.

Lời giải:

a)

Với mọi x > 3, ta có x – 3 > 0 nên |x – 3| = x – 3.

Do đó,

b) $\underset{x\to 1^{-}}{\lim }\frac{x}{\sqrt{1-x}}$

Ta có: $\underset{x\to 1^{-}}{\lim }x=1>0$; $\underset{x\to 1^{-}}{\lim }\sqrt{1-x}=0$

Và với mọi x < 1, ta có 1 – x > 0, suy ra $\sqrt{1-x}>0$.

Vậy $\underset{x\to 1^{-}}{\lim }\frac{x}{\sqrt{1-x}}=+\infty$.

Bài 5.30 trang 124 Toán 11 Tập 1: Chứng minh rằng giới hạn 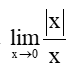không tồn tại.

Lời giải:

+) Với x > 0, ta có: |x| = x.

Khi đó, 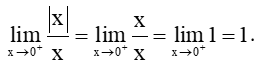(1)

+) Với x < 0, ta có: |x| = – x.

Khi đó, 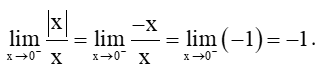(2)

Từ (1) và (2) suy ra 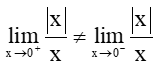nên không tồn tại giới hạn

Bài 5.31 trang 124 Toán 11 Tập 1: Giải thích tại sao các hàm số sau đây gián đoạn tại điểm đã cho.

Lời giải:

a) Với x ≠ 0, thì $f\left(x\right)=\frac{1}{x}$, ta có: $\underset{x\to 0^{-}}{\lim }\frac{1}{x}=-\infty$ và $\underset{x\to 0^{+}}{\lim }\frac{1}{x}=+\infty$.

Suy ra $\underset{x\to 0^{-}}{\lim }\frac{1}{x}\ne \underset{x\to 0^{+}}{\lim }\frac{1}{x}$ nên không tồn tại $\underset{x\to 0}{\lim }\frac{1}{x}$.

Vậy hàm số đã cho gián đoạn tại x = 0.

b) Ta có: $\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\left(2-x\right)=2-1=1$;

$\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(1+x\right)=1+1=2$.

Suy ra nên không tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$.

Vậy hàm số đã cho gian đoạn tại x = 1.

Bài 5.32 trang 124 Toán 11 Tập 1: Lực hấp dẫn tác dụng lên một đơn vị khối lượng ở khoảng cách r tính từ tâm Trái Đất là

trong đó M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn. Xét tính liên tục của hàm số F(r).

Lời giải:

Vì M và R lần lượt là khối lượng và bán kính của Trái Đất, G là hằng số hấp dẫn, do đó M, R, G đều khác 0, r là khoảng cách nên r > 0.

Ta có: 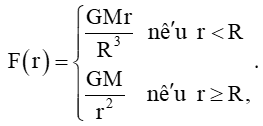Tập xác định của hàm số F(r) là (0; +∞).

+) Với r < R thì F(r) = $\frac{GMr}{R^3}$ hay F(r) = $\frac{GM}{R^3}.r$ là hàm đa thức nên nó liên tục trên (0; R).

+) Với r > R thì F(r) = $\frac{GM}{r^2}$ là hàm phân thức nên nó liên tục trên (R; +∞).

+) Tại r = R, ta có F(R) = $\frac{GM}{R^2}$.

$\underset{r\to R^{+}}{\lim }F\left(r\right)=\underset{r\to R^{+}}{\lim }\frac{GM}{r^2}=\frac{GM}{R^2}$; $\underset{r\to R^{-}}{\lim }f\left(R\right)=\underset{r\to R^{-}}{\lim }\frac{GMr}{R^3}=\frac{GMR}{R^3}=\frac{GM}{R^2}$.

Do đó, $\underset{r\to R^{+}}{\lim }F\left(r\right)=\underset{r\to R^{-}}{\lim }F\left(r\right)=\frac{GM}{R^2}$ nên $\underset{r\to R}{\lim }F\left(r\right)=\frac{GM}{R^2}=F\left(R\right)$.

Suy ra hàm số F(r) liên tục tại r = R.

Vậy hàm số F(r) liên tục trên (0; +∞).

Bài 5.33 trang 124 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau và giải thích tại sao các hàm này liên tục trên các khoảng xác định của chúng.

a) $f\left(x\right)=\frac{\cos x}{x^2+5x+6}$;

b) $g\left(x\right)=\frac{x-2}{\sin x}$.

Lời giải:

a) Biểu thức có nghĩa khi x² + 5x + 6 ≠ 0 ⇔ (x + 2)(x + 3) ≠ 0

Do đó, tập xác định của hàm số f(x) là ℝ \ {– 3; – 2} = (–∞; – 3) ∪ (– 3; – 2) ∪ (– 2; +∞).

Suy ra hàm số f(x) xác định trên các khoảng (–∞; – 3), (– 3; – 2) và (– 2; +∞). Trên các khoảng này, tử thức (hàm lượng giác) và mẫu thức (hàm đa thức) là các hàm số liên tục. Vậy hàm số $f\left(x\right)=\frac{\cos x}{x^2+5x+6}$ liên tục trên các khoảng xác định của chúng.

b) Biểu thức $\frac{x-2}{\sin x}$ có nghĩa khi sin x ≠ 0 ⇔ x ≠ kπ, k ∈ ℤ.

Do đó, tập xác định của hàm số g(x) là ℝ \ {kπ | k ∈ ℤ}.

Trên các khoảng xác định của hàm số g(x), tử thức x – 2 (hàm đa thức) và mẫu thức sin x (hàm lượng giác) là các hàm số liên tục.

Vậy hàm số $g\left(x\right)=\frac{x-2}{\sin x}$ liên tục trên các khoảng xác định của chúng.

Bài 5.34 trang 124 Toán 11 Tập 1: Tìm các giá trị của a để hàm số liên tục trên ℝ.

Lời giải:

Ta có: 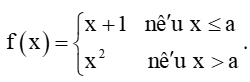Tập xác định của hàm số f(x) là ℝ.

+) Với x < a thì f(x) = x + 1 là hàm đa thức nên nó liên tục trên (–∞; a).

+) Với x > a thì f(x) = x² là hàm đa thức nên nó liên tục trên (a; +∞).

+) Tại x = a, ta có f(a) = a + 1.

$\underset{x\to a^{-}}{\lim }f\left(x\right)=\underset{x\to a^{-}}{\lim }\left(x+1\right)=a+1$; $\underset{x\to a^{+}}{\lim }f\left(x\right)=\underset{x\to a^{+}}{\lim }{x}^2=a^2$.

Để hàm số f(x) đã cho liên tục trên ℝ thì f(x) phải liên tục tại x = a, điều này xảy ra khi và chỉ khi $\underset{x\to a^{+}}{\lim }f\left(x\right)=\underset{x\to a^{-}}{\lim }f\left(x\right)=f\left(a\right)$⇔ a + 1 = a² ⇔ a² – a – 1 = 0

Suy ra $a=\frac{1-\sqrt{5}}{2}$ hoặc $a=\frac{1+\sqrt{5}}{2}$.

Vậy thì thỏa mãn yêu cầu bài toán.

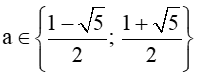
Lời giải bài tập Toán 11 Bài tập cuối Chương 5 Kết nối tri thức hay khác:

• Giải Toán 11 trang 123