Giải Toán 11 trang 23 Tập 1 Kết nối tri thức

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 23 Tập 1 trong Bài 3: Hàm số lượng giác Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 23.

Giải Toán 11 trang 23 Tập 1 Kết nối tri thức

Luyện tập 1 trang 23 Toán 11 Tập 1: Tìm tập xác định của hàm số $y=\frac{1}{\sin x}.$

Lời giải:

Biểu thức $\frac{1}{\sin x}$  có nghĩa khi sin x ≠ 0, tức là x ≠ kπ (k ∈ ℤ).

Vậy tập xác định của hàm số $y=\frac{1}{\sin x}$ là ℝ \ {kπ | k ∈ ℤ}.

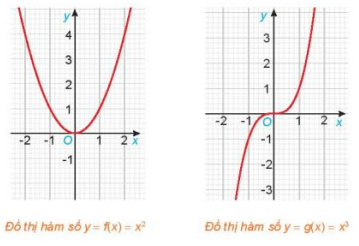
HĐ2 trang 23 Toán 11 Tập 1: Cho hai hàm số f(x) = x² và g(x) = x³, với các đồ thị như hình dưới đây.

a) Tìm các tập xác định D_f, D_g của các hàm số f(x) và g(x).

b) Chứng tỏ rằng f(– x) = f(x), ∀ x ∈ D_f. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = f(x) đối với hệ trục tọa độ Oxy?

c) Chứng tỏ rằng g(– x) = – g(x), ∀ x ∈ D_g. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục tọa độ Oxy?

Lời giải:

a) Biểu thức x² và x³ luôn có nghĩa với mọi x ∈ ℝ.

Vậy tập xác định của hàm số f(x) = x² là D_f = ℝ và tập xác định của hàm số g(x) = x³ là D_g = ℝ.

b) ∀ x ∈ D_f, ta luôn có f(– x) = (– x)² = x² = f(x). Vậy f(– x) = f(x), ∀ x ∈ D_f.

Từ hình vẽ ta thấy đồ thị hàm số f(x) = x² đối xứng với nhau qua trục tung Oy.

c) ∀ x ∈ D_g, ta luôn có g(– x) = (– x)³ = – x³ = – g(x). Vậy g(– x) = – g(x), ∀ x ∈ D_g.

Từ hình vẽ ta thấy đồ thị hàm số g(x) = x³ nhận gốc tọa độ O làm tâm đối xứng.

Lời giải bài tập Toán 11 Bài 3: Hàm số lượng giác Kết nối tri thức hay khác:

• Giải Toán 11 trang 22
• Giải Toán 11 trang 24
• Giải Toán 11 trang 25
• Giải Toán 11 trang 26
• Giải Toán 11 trang 27
• Giải Toán 11 trang 29
• Giải Toán 11 trang 30