Giải Toán 11 trang 30 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 30 Tập 1 trong Bài 3: Hàm số lượng giác Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 30.

Giải Toán 11 trang 30 Tập 1 Kết nối tri thức

Luyện tập 7 trang 30 Toán 11 Tập 1: Sử dụng đồ thị đã vẽ ở Hình 1.17, hãy xác định các giá trị của x trên đoạn $\left[-\frac{\pi }{2};2\pi \right]$  để hàm số y = cot x nhận giá trị dương.

Lời giải:

Hàm số y = cot x nhận giá trị dương ứng với phần đồ thị nằm trên trục hoành. Từ đồ thị ở Hình 1.17 ta suy ra trên đoạn $\left[-\frac{\pi }{2};2\pi \right]$  thì y > 0 khi $x\in \left(0;\frac{\pi }{2}\right)\cup \left(\pi ;\frac{3\pi }{2}\right)$ .

Bài 1.14 trang 30 Toán 11 Tập 1: Tìm tập xác định của các hàm số sau:

a) $y=\frac{1-\cos x}{\sin x}$ ;

b) $y=\sqrt{\frac{1+\cos x}{2-\cos x}}$ .

Lời giải:

a) Biểu thức $\frac{1-\cos x}{\sin x}$ có nghĩa khi sin x ≠ 0, tức là x ≠ kπ, k ∈ ℤ.

Vậy tập xác định của hàm số $y=\frac{1-\cos x}{\sin x}$ là D = ℝ \ {kπ | k ∈ ℤ}.

b) Biểu thức $\sqrt{\frac{1+\cos x}{2-\cos x}}$ có nghĩa khi $\left\{\begin{array}{l}\frac{1+\cos x}{2-\cos x}\ge 0\\ 2-\cos x\ne 0\end{array}\right.$.

Vì – 1 ≤ cos x ≤ 1 nên 1 + cos x ≥ 0 với mọi x ∈ ℝ và 2 – cos x ≥ 1 > 0 với mọi x ∈ ℝ.

Do đó, 2 – cos x ≠ 0 với mọi x ∈ ℝ và $\frac{1+\cos x}{2-\cos x}\ge 0$  với mọi x ∈ ℝ.

Vậy tập xác định của hàm số $y=\sqrt{\frac{1+\cos x}{2-\cos x}}$  là D = ℝ.

Bài 1.15 trang 30 Toán 11 Tập 1: Xét tính chẵn lẻ của các hàm số sau:

a) y = sin 2x + tan 2x;

b) y = cos x + sin² x;

c) y = sin x cos 2x;

d) y = sin x + cos x.

Lời giải:

a) Biểu thức sin 2x + tan 2x có nghĩa khi cos 2x ≠ 0 (do $\tan 2x=\frac{\sin 2x}{\cos 2x}$ ), tức là $2x\ne \frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$$\iff x\ne \frac{\pi }{4}+k\frac{\pi }{2},k\in \mathbb{Z}$.

Suy ra tập xác định của hàm số y = f(x) = sin 2x + tan 2x là $D=ℝ\backslash \left\{\frac{\pi }{4}+k\frac{\pi }{2}|k\in \mathbb{Z}\right\}$ .

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– 2x) + tan (– 2x) = – sin 2x – tan 2x = – (sin 2x + tan 2x) = – f(x), ∀ x ∈ D.

Vậy y = sin 2x + tan 2x là hàm số lẻ.

b) Tập xác định của hàm số y = f(x) = cos x + sin² x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = cos (– x) + sin² (– x) = cos x + (– sin x)² = cos x + sin² x = f(x), ∀ x ∈ D.

Vậy y = cos x + sin² x là hàm số chẵn.

c) Tập xác định của hàm số y = f(x) = sin x cos 2x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– x) . cos (– 2x) = – sin x . cos 2x = – f(x), ∀ x ∈ D.

Vậy y = sin x cos 2x là hàm số lẻ.

d) Tập xác định của hàm số y = f(x) = sin x + cos x là D = ℝ.

Do đó, nếu x thuộc tập xác định D thì – x cũng thuộc tập xác định D.

Ta có: f(– x) = sin (– x) + cos (– x) = – sin x + cos x ≠ – f(x).

Vậy y = sin x + cos x là hàm số không chẵn, không lẻ.

Bài 1.16 trang 30 Toán 11 Tập 1: Tìm tập giá trị của các hàm số sau:

a) y = $2\sin \left(x-\frac{\pi }{4}\right)-1$ ;

b) y = $\sqrt{1+\cos x}-2$.

Lời giải:

a) Ta có: $-1\le \sin \left(x-\frac{\pi }{4}\right)\le 1$ với mọi x ∈ ℝ

$\iff -2\le 2\sin \left(x-\frac{\pi }{4}\right)\le 2$ với mọi x ∈ ℝ

$\iff -2-1\le 2\sin \left(x-\frac{\pi }{4}\right)-1\le 2-1$ với mọi x ∈ ℝ

$\iff -3\le 2\sin \left(x-\frac{\pi }{4}\right)-1\le 1$ với mọi x ∈ ℝ

⇔ – 3 ≤ y ≤ 1 với mọi x ∈ ℝ.

Vậy tập giá trị của hàm số y = $2\sin \left(x-\frac{\pi }{4}\right)-1$ là [– 3; 1].

b) Vì – 1 ≤ cos x ≤ 1 với mọi x ∈ ℝ nên 0 ≤ 1 + cos x ≤ 2 với mọi x ∈ ℝ.

Do đó, $0\le \sqrt{1+\cos x}\le \sqrt{2}$ với mọi x ∈ ℝ.

Suy ra $-2\le \sqrt{1+\cos x}-2\le \sqrt{2}-2$  với mọi x ∈ ℝ.

Hay $-2\le y\le \sqrt{2}-2$ với mọi x ∈ ℝ.

Vậy tập giá trị của hàm số y = $\sqrt{1+\cos x}-2$ là $\left[-2;\sqrt{2}-2\right]$ .

Bài 1.17 trang 30 Toán 11 Tập 1: Từ đồ thị của hàm số y = tan x, hãy tìm các giá trị x sao cho tan x = 0.

Lời giải:

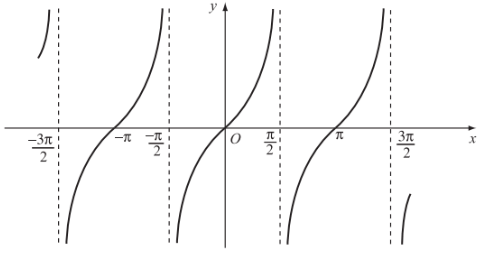
Ta có đồ thị của hàm số y = tan x như hình vẽ dưới đây.

Ta có tan x = 0 khi hàm số y = tan x nhận giá trị bằng 0 ứng với các điểm x mà đồ thị giao với trục hoành. Từ đồ thị ở hình trên ta suy ra y = 0 hay tan x = 0 khi x = kπ, k ∈ ℤ. 

Bài 1.18 trang 30 Toán 11 Tập 1: Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số h(t) = $90\cos \left(\frac{\pi }{10}t\right)$, trong đó h(t) là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm t giây.

a) Tìm chu kì của sóng.

b) Tìm chiều cao của sóng, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.

Lời giải:

a) Chu kì của sóng là $T=\frac{2\pi }{\frac{\pi }{10}}=20$ (giây).

b) Chiều cao của sóng tức là chiều cao của nước đạt được trong một chu kì dao động.

Ta có: h(20) = $90\cos \left(\frac{\pi }{10}.20\right)$ = 90 (cm).

Vậy chiều cao của sóng là 90 cm.

Lời giải bài tập Toán 11 Bài 3: Hàm số lượng giác Kết nối tri thức hay khác:

• Giải Toán 11 trang 22
• Giải Toán 11 trang 23
• Giải Toán 11 trang 24
• Giải Toán 11 trang 25
• Giải Toán 11 trang 26
• Giải Toán 11 trang 27
• Giải Toán 11 trang 29