Giải Toán 11 trang 34 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với Giải Toán 11 trang 34 Tập 1 trong Bài 4: Phương trình lượng giác cơ bản Toán lớp 11 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 11 trang 34.

Giải Toán 11 trang 34 Tập 1 Kết nối tri thức

Luyện tập 2 trang 34 Toán 11 Tập 1: Giải các phương trình sau:

a) $\sin x=\frac{\sqrt{2}}{2}$;

b) sin 3x = – sin 5x.

Lời giải:

a) $\sin x=\frac{\sqrt{2}}{2}$

$\iff \sin x=\sin \frac{\pi }{4}$

$\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k2\pi \\ x=\pi -\frac{\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=\frac{\pi }{4}+k2\pi \\ x=\frac{3\pi }{4}+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình $\sin x=\frac{\sqrt{2}}{2}$ có các nghiệm là $x=\frac{\pi }{4}+k2\pi ,k\in \mathbb{Z}$ và $x=\frac{3\pi }{4}+k2\pi$, $k\in \mathbb{Z}$.

b) sin 3x = – sin 5x

⇔ sin 3x = sin (– 5x)

$\iff \left[\begin{array}{l}3x=-5x+k2\pi \\ 3x=\pi -\left(-5x\right)+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}3x=-5x+k2\pi \\ 3x=\pi +5x+k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}8x=k2\pi \\ -2x=\pi +k2\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

$\iff \left[\begin{array}{l}x=k\frac{\pi }{4}\\ x=-\frac{\pi }{2}+k\pi \end{array}\right.\left(k\in \mathbb{Z}\right)$

Vậy phương trình đã cho có các nghiệm là $x=k\frac{\pi }{4},k\in \mathbb{Z}$ và $x=-\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}$.

HĐ3 trang 34 Toán 11 Tập 1: Nhận biết công thức nghiệm của phương trình cos x = $-\frac{1}{2}$

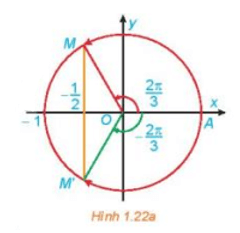
a) Quan sát Hình 1.22a, tìm các nghiệm của phương trình đã cho trong nửa khoảng [– π; π).

b) Dựa vào tính tuần hoàn của hàm số côsin, hãy viết công thức nghiệm của phương trình đã cho.

Lời giải:

a) Từ Hình 1.22a, nhận thấy hai điểm M, M' lần lượt biểu diễn các góc $\frac{2\pi }{3}$ và $-\frac{2\pi }{3}$, lại có hoành độ của điểm M và M' đều bằng $-\frac{1}{2}$ nên theo định nghĩa giá trị lượng giác, ta có $\cos \frac{2\pi }{3}=-\frac{1}{2}$ và $\cos \left(-\frac{2\pi }{3}\right)=-\frac{1}{2}$.

Vậy trong nửa khoảng [– π; π), phương trình $\cos x=-\frac{1}{2}$ có hai nghiệm là $x=\frac{2\pi }{3}$, $x=-\frac{2\pi }{3}$.

b) Vì hàm số cos có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là $x=\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$ và $x=-\frac{2\pi }{3}+k2\pi ,k\in \mathbb{Z}$.

Lời giải bài tập Toán 11 Bài 4: Phương trình lượng giác cơ bản Kết nối tri thức hay khác:

• Giải Toán 11 trang 31
• Giải Toán 11 trang 32
• Giải Toán 11 trang 35
• Giải Toán 11 trang 36
• Giải Toán 11 trang 37
• Giải Toán 11 trang 39