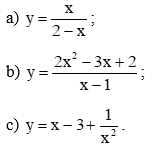Bài 4 trang 27 Toán 12 Tập 1 Cánh diều

---

Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Cánh diều

Bài 4 trang 27 Toán 12 Tập 1: Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:

Lời giải:

a) Hàm số đã cho có tập xác định là ℝ\{2}.

● Ta có $\underset{x\to 2^{-}}{\lim }$$\frac{x}{2 - x}= +\infty$, $\underset{x\to 2^{+}}{\lim }$$\frac{x}{2 - x}= -\infty$ .

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số đã cho.

● Lại có $\underset{x\to +\infty }{\lim }$ $\frac{x}{2 - x}= -1$, $\underset{x\to -\infty }{\lim }$$\frac{x}{2 - x}= -1$.

Do đó, đường thẳng y = – 1 là tiệm cận ngang của đồ thị hàm số đã cho.

● Ta có $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{x}{(2 - x) x}$= $\underset{x\to +\infty }{\lim }$$\frac{1}{2 - x}$= $-\infty$ .

Do đó, đồ thị hàm số y = $\frac{x}{2 - x}$  không có tiệm cận xiên.

b) Hàm số đã cho có tập xác định là ℝ\{1}.

● Ta có $\underset{x\to 1^{+}}{\lim }$$\frac{2x^2 + x + 1}{x - 1}= +\infty$; $\underset{x\to 1-}{\lim }$= $\frac{2x^2 + x + 1}{x - 1}= -\infty$.

Do đó, đường thẳng x = 1 tiệm cận đứng của đồ thị hàm số đã cho.

● Lại có $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x - 1}= +\infty$; $\underset{x\to -\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x - 1}= -\infty$ .

Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.

● Tiệm cận xiên của đồ thị hàm số đã cho có dạng y = ax + b.

Ta có:  a = $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x (x - 1)}$= 2

và b = $\underset{x\to +\infty }{\lim }$[y - 2x]= $\underset{x\to +\infty }{\lim }$$\left(\frac{2x^2 - 3x + 2}{x - 1} - 2x\right)$= $\underset{x\to +\infty }{\lim }$$\frac{-x + 2}{x - 1}$= -1 .

Vậy đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).

Tương tự, do $\underset{x\to -\infty }{\lim }$$\frac{y}{x}= 2$  và $\underset{x\to -\infty }{\lim }$[y - 2x] = -1  nên đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).

c) Hàm số đã cho có tập xác định là ℝ\{0}.

● Ta có $\underset{x\to 0^{+}}{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$ = +$\infty$;$\underset{x\to 0^{-}}{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= - $\infty$.

Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số đã cho.

● Lại có $\underset{x\to +\infty }{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= + $\infty$; $\underset{x\to -\infty }{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= - $\infty$.

Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.

● Do $\underset{x\to +\infty }{\lim }$[y - (x - 3)] = $\underset{x\to +\infty }{\lim }$$\frac{1}{x^2}$= 0; $\underset{x\to -\infty }{\lim }$[y - (x - 3)] = $\underset{x\to -\infty }{\lim }$$\frac{1}{x^2}$= 0  nên đường thẳng y = x – 3 là tiệm cận xiên của đồ thị hàm số đã cho.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

• Câu hỏi khởi động trang 21 Toán 12 Tập 1: Số dân của một thị trấn sau x năm kể từ năm 1970 được ước tính bởi công thức ....

• Hoạt động 1 trang 21 Toán 12 Tập 1: Xét hàm số y = f(x) = $\frac{26x + 10}{x + 5}$ , với x ∈ [0; + ∞) có đồ thị là đường cong ở Hình 10 trong bài toán mở đầu....

• Luyện tập 1 trang 22 Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y = \frac{3x - 2}{x + 1}$...

• Hoạt động 2 trang 22 Toán 12 Tập 1: Cho hàm số y = f(x) = $\frac{1}{x}$ có đồ thị là đường cong như Hình 12.....

• Luyện tập 2 trang 23 Toán 12 Tập 1: Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x^2 + 3x}{x - 5}$....

• Hoạt động 3 trang 24 Toán 12 Tập 1: Cho hàm số y = f(x) = $x + 1 + \frac{1}{x - 1}$ có đồ thị là (C) và đường thẳng y = x + 1 (Hình 15).....

• Luyện tập 3 trang 25 Toán 12 Tập 1: Chứng minh rằng đường thẳng y = – x là tiệm cận xiên của đồ thị hàm số y = f(x) = $\frac{-x^2 - 2x +3}{x + 2}$. ...

• Luyện tập 4 trang 26 Toán 12 Tập 1: Tìm tiệm cận xiên của đồ thị hàm số $y = f\left(x\right) = \frac{x^2 -3x + 2}{x + 3}$ ....

• Bài 1 trang 27 Toán 12 Tập 1: Tiệm cận đứng của đồ thị hàm số $y = \frac{x+ 2}{x + 1}$ là:....

• Bài 2 trang 27 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y = \frac{x^2+3x +5}{x + 2}$ là:....

• Bài 3 trang 27 Toán 12 Tập 1: Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau? ....

• Bài 5 trang 27 Toán 12 Tập 1: Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức $S\left(x\right) = 200\left(5 - \frac{9}{2 + x}\right)$,...