Giải Toán 12 trang 16 Tập 1 Cánh diều

---

Với Giải Toán 12 trang 16 Tập 1 trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 16.

Giải Toán 12 trang 16 Tập 1 Cánh diều

Luyện tập 1 trang 16 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số $f\left(x\right) =\sqrt{9 -x^2}$ trên đoạn [– 3; 3]

Lời giải:

Do 0 ≤ x² ≤ 9 với mọi x ∈ [– 3; 3] nên – 9 ≤ – x² ≤ 0 với mọi x ∈ [– 3; 3], khi đó ta suy ra 0 ≤ 9 – x² ≤ 9 với mọi x ∈ [– 3; 3], do đó $0\le \sqrt{9 - x^2}\le 3$  với mọi x ∈ [– 3; 3], tức là 0 ≤ f(x) ≤ 3 với mọi x ∈ [– 3; 3].

Ta có f(0) = 3 nên $\underset{[-3; 3]}{max}$f(x) = 3; f(3) = f(– 3) = 0 nên $\underset{[-3; 3]}{min}$f(x) = 0.

Hoạt động 2 trang 16 Toán 12 Tập 1: Cho hàm số $f\left(x\right) = x + \frac{1}{x -1}$ với x > 1

a) Tính $\underset{x\to 1^{+}}{\lim f\left(x\right)}$, $\underset{x\to +\infty }{\lim f\left(x\right)}$ .

b) Lập bảng biến thiên của hàm số f(x) trên khoảng (1; + ∞).

c) Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số f(x) trên khoảng (1; +∞).

Lời giải:

Ta có f(x) =x + $\frac{1}{x - 1} = \frac{x^2 - x +1}{x - 1}$

a) Ta có $\underset{x\to 1^{+}}{\lim }$($x^2 -x + 1)$ = 1 >0,$\underset{x\to 1^{+}}{\lim }$(x - 1) =0 , x – 1 > 0 khi x → 1⁺.

Do đó,$\underset{x\to 1^{+}}{\lim }$f(x) = +$\infty$ .

Ta có $\underset{x\to +\infty }{\lim }$f(x)= $\underset{x\to +\infty }{\lim }$$\frac{x^2-x +1}{x - 1}$= $\underset{x\to +\infty }{\lim }$$\left(x.\frac{1 - {\displaystyle \frac{1}{x}} + {\displaystyle \frac{1}{x^2}}}{1 - {\displaystyle \frac{1}{x}}}\right)$ = $+ \infty$.

b) Ta có f'(x) = 1 - $\frac{1}{{(x -1)}^2}$ với x > 1.

          f'(x) = 0 ⇔ (x – 1)² = 1 ⇔ x = 2 (t/m) hoặc x = 0 (loại).

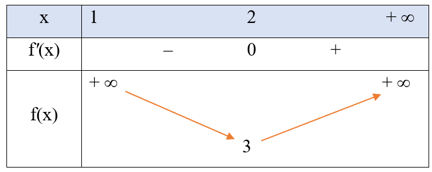
Bảng biến thiên của hàm số f(x) trên khoảng (1; + ∞) như sau:

c) Từ bảng biến thiên ta suy ra hàm số f(x) có giá trị nhỏ nhất trên khoảng (1; + ∞) là 3 tại x = 2 và hàm số này không có giá trị lớn nhất trên khoảng (1; + ∞).

Luyện tập 2 trang 16 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số $y = \frac{2x - 5}{x - 1}$ trên nửa khoảng (1; 3]

Lời giải:

● Xét hàm số $y = \frac{2x - 5}{x -1}$  với x ∈ (1; 3].

● Ta có: $y\text{'} = \frac{3}{{(x - 1)}^2}$ .

          y' > 0 với mọi x ∈ (1; 3].

Ngoài ra $\underset{x\to 1^{+}}{\lim }$y = -$\infty$, $\underset{x\to 3^{-}}{\lim }$y = y(3) = $\frac{1}{2}$.

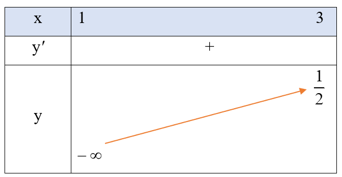
Bảng biến thiên của hàm số như sau:

Từ bảng biến thiên suy ra $\underset{(1; 3]}{max }$y = $\frac{1}{2}$ tại x = 3 và hàm số y không có giá trị lớn nhất.

Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác:

• Giải Toán 12 trang 15
• Giải Toán 12 trang 20