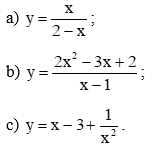Giải Toán 12 trang 27 Tập 1 Cánh diều

---

Với Giải Toán 12 trang 27 Tập 1 trong Bài 3: Đường tiệm cận của đồ thị hàm số Toán 12 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 27.

Giải Toán 12 trang 27 Tập 1 Cánh diều

Bài 1 trang 27 Toán 12 Tập 1: Tiệm cận đứng của đồ thị hàm số $y = \frac{x+ 2}{x + 1}$ là:

A. x = – 1.

B. x = – 2.

C. x = 1.

D. x = 2. 

Lời giải:

Đáp án đúng là: A

Hàm số đã cho có tập xác định là ℝ\{– 1}.

Ta có $\underset{x\to 1^{+}}{\lim }$y = $\underset{x\to 1^{+}}{\lim }$$\frac{x + 2}{x + 1}$= +$\infty$; $\underset{x\to 1^{-}}{\lim }$y = $\underset{x\to 1^{-}}{\lim }$$\frac{x + 2}{x + 1}$= - $\infty$.

Vậy đường thẳng x = – 1 là tiệm cận đứng của đồ thị hàm số đã cho.

Bài 2 trang 27 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y = \frac{x^2+3x +5}{x + 2}$ là:

A. y = x.

B. y = x + 1.

C. y = x + 2.

D. y = x + 3.

Lời giải:

Đáp án đúng là: B

Ta có: a = $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{x^2+ 3x + 5}{x (x + 2)}$ = 1

và b = $\underset{x\to +\infty }{\lim }$[y - x] = $\underset{x\to +\infty }{\lim }$$\left(\frac{x^2+ 3x + 5}{x + 2} - x\right)$= $\underset{x\to +\infty }{\lim }$$\frac{x + 5}{x + 2}$= 1 .

Vậy đường thẳng y = x + 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).

Tương tự, do $\underset{x\to -\infty }{\lim }$$\frac{y}{x}$= 1  và $\underset{x\to -\infty }{\lim }$[y - x] = 1 nên đường thẳng y = x + 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).

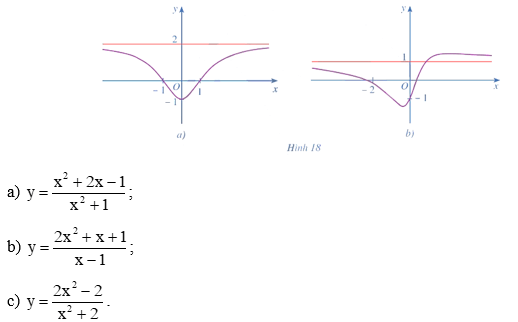
Bài 3 trang 27 Toán 12 Tập 1: Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

Lời giải:

Ta có $\underset{x\to +\infty }{\lim }$$\frac{x^2 + 2x -1}{x^2 + 1}$= 1; $\underset{x\to +\infty }{\lim }$$\frac{2x^2+ x + 1}{x - 1}= +\infty$; $\underset{x\to +\infty }{\lim }$$\frac{2x^2- 2}{x^2 + 2}= 2$.

● Xét đồ thị ở Hình 18a, ta thấy đường thẳng y = 2 là tiệm cận ngang của đồ thị này.

Lại có $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 2}{x^2 + 2}$= 2, vậy đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số y =$\frac{2x^2- 2}{x^2 + 2}$ . Khi đó, đồ thị hàm số ở Hình 18a là đồ thị của hàm số .

● Xét đồ thị ở Hình 18b, ta thấy đường thẳng y = 1 là tiệm cận ngang của đồ thị này.

Lại có $\underset{x\to +\infty }{\lim }$$\frac{x^2 + 2x -1}{x^2 + 1}$ = 1, vậy đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = $\frac{x^2 + 2x -1}{x^2 + 1}$ . Khi đó, đồ thị hàm số ở Hình 18b là đồ thị của hàm số y = $\frac{x^2 + 2x -1}{x^2 + 1}$ .

Bài 4 trang 27 Toán 12 Tập 1: Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:

Lời giải:

a) Hàm số đã cho có tập xác định là ℝ\{2}.

● Ta có $\underset{x\to 2^{-}}{\lim }$$\frac{x}{2 - x}= +\infty$, $\underset{x\to 2^{+}}{\lim }$$\frac{x}{2 - x}= -\infty$ .

Do đó, đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số đã cho.

● Lại có $\underset{x\to +\infty }{\lim }$ $\frac{x}{2 - x}= -1$, $\underset{x\to -\infty }{\lim }$$\frac{x}{2 - x}= -1$.

Do đó, đường thẳng y = – 1 là tiệm cận ngang của đồ thị hàm số đã cho.

● Ta có $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{x}{(2 - x) x}$= $\underset{x\to +\infty }{\lim }$$\frac{1}{2 - x}$= $-\infty$ .

Do đó, đồ thị hàm số y = $\frac{x}{2 - x}$  không có tiệm cận xiên.

b) Hàm số đã cho có tập xác định là ℝ\{1}.

● Ta có $\underset{x\to 1^{+}}{\lim }$$\frac{2x^2 + x + 1}{x - 1}= +\infty$; $\underset{x\to 1-}{\lim }$= $\frac{2x^2 + x + 1}{x - 1}= -\infty$.

Do đó, đường thẳng x = 1 tiệm cận đứng của đồ thị hàm số đã cho.

● Lại có $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x - 1}= +\infty$; $\underset{x\to -\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x - 1}= -\infty$ .

Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.

● Tiệm cận xiên của đồ thị hàm số đã cho có dạng y = ax + b.

Ta có:  a = $\underset{x\to +\infty }{\lim }$$\frac{y}{x}$= $\underset{x\to +\infty }{\lim }$$\frac{2x^2 - 3x + 2}{x (x - 1)}$= 2

và b = $\underset{x\to +\infty }{\lim }$[y - 2x]= $\underset{x\to +\infty }{\lim }$$\left(\frac{2x^2 - 3x + 2}{x - 1} - 2x\right)$= $\underset{x\to +\infty }{\lim }$$\frac{-x + 2}{x - 1}$= -1 .

Vậy đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → + ∞).

Tương tự, do $\underset{x\to -\infty }{\lim }$$\frac{y}{x}= 2$  và $\underset{x\to -\infty }{\lim }$[y - 2x] = -1  nên đường thẳng y = 2x – 1 là tiệm cận xiên của đồ thị hàm số đã cho (khi x → – ∞).

c) Hàm số đã cho có tập xác định là ℝ\{0}.

● Ta có $\underset{x\to 0^{+}}{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$ = +$\infty$;$\underset{x\to 0^{-}}{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= - $\infty$.

Do đó, đường thẳng x = 0 là tiệm cận đứng của đồ thị hàm số đã cho.

● Lại có $\underset{x\to +\infty }{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= + $\infty$; $\underset{x\to -\infty }{\lim }$$\left(x - 3 + \frac{1}{x^2}\right)$= - $\infty$.

Do đó, đồ thị hàm số đã cho không có tiệm cận ngang.

● Do $\underset{x\to +\infty }{\lim }$[y - (x - 3)] = $\underset{x\to +\infty }{\lim }$$\frac{1}{x^2}$= 0; $\underset{x\to -\infty }{\lim }$[y - (x - 3)] = $\underset{x\to -\infty }{\lim }$$\frac{1}{x^2}$= 0  nên đường thẳng y = x – 3 là tiệm cận xiên của đồ thị hàm số đã cho.

Bài 5 trang 27 Toán 12 Tập 1: Số lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức $S\left(x\right) = 200\left(5 - \frac{9}{2 + x} \right)$ , trong đó x ≥ 1 (Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014).

a) Xem y = S(x) là một hàm số xác định trên nửa khoảng [1; + ∞), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn. 

Lời giải:

a) Xét hàm số y = S(x) = 200$\left(5 - \frac{9}{2 + x}\right)$  với x ∈ [1; + ∞).

Ta có $\underset{x\to +\infty }{\lim }$y = $\underset{x\to +\infty }{\lim }$200$\left(5 - \frac{9}{2 + x}\right)$= 1000; $\underset{x\to -\infty }{\lim }$= 200$\left(5 - \frac{9}{2 + x}\right)$ = 1000.

Do đó, đường thẳng y = 1 000 là tiệm cận ngang của đồ thị hàm số đã cho trên nửa khoảng [1; + ∞).

b) Ta có đồ thị hàm số y = S(x) với x ∈ [1; + ∞) nhận đường thẳng y = 1 000 làm tiệm cận ngang, tức là khi x càng lớn thì số lượng sản phẩm bán được của công ty đó trong x (tháng) sẽ tiến gần đến 1 000 sản phẩm.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay khác:

• Giải Toán 12 trang 21
• Giải Toán 12 trang 22