Giải Toán 12 trang 48 Tập 1 Cánh diều
Với Giải Toán 12 trang 48 Tập 1 trong Bài tập cuối chương 1 Toán 12 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 48.
Giải Toán 12 trang 48 Tập 1 Cánh diều
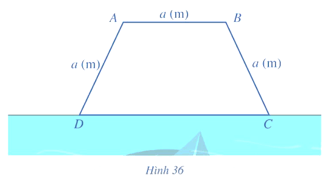
Bài 12 trang 48 Toán 12 Tập 1: Một bác nông dân có ba tấm lưới thép B40, mỗi tấm dài a (m) và muốn rào một mảnh vườn dọc bờ sông có dạng hình thang cân ABCD như Hình 36 (bờ sông là đường thẳng CD không phải rào). Hỏi bác đó có thể rào được mảnh vườn có diện tích lớn nhất là bao nhiêu mét vuông?
Lời giải:
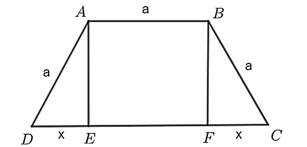
Dựng các đường cao AE và BF của hình thang cân ABCD như hình vẽ trên.
Vì ABCD là hình thang cân nên DE = FC và EF = AB = a.
Đặt DE = FC = x (m) (x > 0).
Ta có DC = DE + EF + FC = x + a + x = 2x + a.
Theo định lí Pythagore, ta suy ra AE = = (m).
Rõ ràng, x phải thỏa mãn điều kiện 0 < x < a.
Diện tích của hình thang cân ABCD là
S = (AB + CD)AE = (a + 2x + a) = (a + x) (m2).
Xét hàm số S(x) = (a + x) với x ∈ (0; a).
Ta có S'(x) = ;
S'(x) = 0 ⇔ – 2x2 – ax + a2 = 0 ⇔ (x + a)(a – 2x) = 0 ⇔ x = – a hoặc x = .
Khi đó trên khoảng (0; a), S'(x) = 0 khi x = .
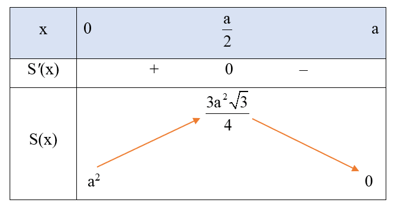
Bảng biến thiên của hàm số S(x) như sau:
Căn cứ vào bảng biến thiên, ta thấy hàm số S(x) đạt giá trị lớn nhất bằng tại .
Vậy bác đó có thể rào được mảnh vườn có diện tích lớn nhất là (m2).
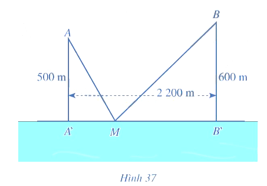
Bài 13 trang 48 Toán 12 Tập 1: Có hai xã cùng ở một bên bờ sông Lam. Người ta đo được khoảng cách từ trung tâm A, B của hai xã đó đến bờ sông lần lượt là AA' = 500 m, BB' = 600 m và A'B' = 2 200 m (Hình 37). Các kĩ sư muốn xây một trạm cung cấp nước sạch nằm bên bờ sông Lam cho người dân hai xã. Để tiết kiệm chi phí, các kĩ sư cần phải chọn vị trí M của trạm cung cấp nước sạch đó trên đoạn A'B' sao cho tổng khoảng cách từ hai vị trí A, B đến vị trí M là nhỏ nhất. Hãy tìm giá trị nhỏ nhất của tổng khoảng cách đó.
Lời giải:
Đặt A'M = x (m).
Suy ra B'M = A'B' – A'M = 2 200 – x (m).
Rõ ràng, x phải thỏa mãn điều kiện 0 < x < 2 200.
Áp dụng định lí Pythagore ta tính được:
AM = = (m);
BM = = (m).
Tổng khoảng cách từ hai vị trí A, B đến vị trí M là
D = AM + BM = + (m).
Xét hàm số D(x) = + với x ∈ (0; 2 200).
Ta có D'(x) = ;
Trên khoảng (0; 2 200), ta thấy D'(x) = 0 khi x = 1 000.
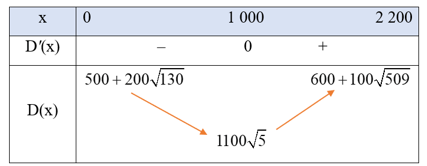
Bảng biến thiên của hàm số D(x) như sau:
Căn cứ vào bảng biến thiên, ta thấy hàm số D(x) đạt giá trị nhỏ nhất bằng tại x = 1 000.
Vậy giá trị nhỏ nhất của tổng khoảng cách cần tìm là m.
Bài 14 trang 48 Toán 12 Tập 1: Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ với giá 2 triệu đồng/1 tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá cho thuê mỗi căn hộ thêm 200 nghìn đồng/1 tháng thì có thêm một căn hộ bị bỏ trống. Hỏi công ty nên cho thuê mỗi căn hộ bao nhiêu tiền một tháng để tổng số tiền thu được là lớn nhất?
Lời giải:
Cứ tăng thêm 200 nghìn đồng vào giá thuê một căn hộ trên một tháng thì có một căn hộ bị bỏ trống.
Gọi số lần tăng 200 nghìn đồng vào giá thuê một căn hộ trên một tháng là x (x ∈ ℕ*).
Khi đó x cũng là số căn hộ bị bỏ trống.
Tổng số tiền công ty thu được lúc này là
T(x) = (2 000 + 200x)(20 – x) = 40 000 + 2 000x – 200x2 (nghìn đồng).
Xét hàm số T(x) = 40 000 + 2 000x – 200x2 với x ∈ ℕ*.
Ta có T'(x) = 2 000 – 400x;
T'(x) = 0 ⇔ 2 000 – 400x = 0 ⇔ x = 5 (thỏa mãn).
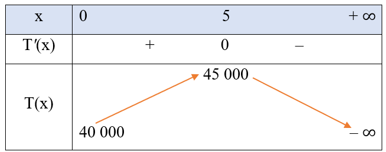
Bảng biến thiên của hàm số T(x) như sau:
Căn cứ vào bảng biến thiên trên, ta thấy hàm số T(x) đạt giá trị lớn nhất bằng 45 000 khi x = 5.
Khi đó, số tiền tăng lên khi cho thuê một căn hộ là 200 ∙ 5 = 1 000 nghìn đồng = 1 triệu đồng.
Vậy công ty nên cho thuê mỗi căn hộ 3 triệu đồng/1 tháng thì tổng số tiền thu được là lớn nhất.
Lời giải bài tập Toán 12 Bài tập cuối chương 1 hay khác: