Giải Toán 12 trang 25 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 12 trang 25 Tập 1 trong Bài 3: Đường tiệm cận của đồ thị hàm số Toán 12 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 25.

Giải Toán 12 trang 25 Tập 1 Chân trời sáng tạo

Bài 4 trang 25 Toán 12 Tập 1: Nồng độ oxygen trong hồ theo thời gian t cho bởi công thức $y\left(t\right)=5-\frac{15t}{9t^2+1}$, với y được tính theo mg/l và t được tính theo giờ, t ≥ 0. Tìm các đường tiệm cận của đồ thị hàm số y = y(t). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn.

Lời giải:

Có $\underset{t\to +\infty }{\lim }y\left(t\right)=\underset{t\to +\infty }{\lim }\left(5-\frac{15t}{9t^2+1}\right)=\underset{t\to +\infty }{\lim }\left(5-\frac{\frac{15}{t}}{9+\frac{1}{t^2}}\right)=5$;

$\underset{t\to -\infty }{\lim }y\left(t\right)=\underset{t\to -\infty }{\lim }\left(5-\frac{15t}{9t^2+1}\right)=\underset{t\to -\infty }{\lim }\left(5-\frac{\frac{15}{t}}{9+\frac{1}{t^2}}\right)=5$

Do đó y = 5 là tiệm cận ngang của đồ thị hàm số và hàm số không có tiệm cận đứng, tiệm cận xiên.

Nhận xét:

Khi thời t trở nên rất lớn, nồng độ oxygen trong hồ sẽ tiến dần về giá trị cố định là 5 mg/l. Điều này có thể được hiểu sau một thời gian dài, môi trường trong hồ sẽ đạt đến một trạng thái ổn định nồng độ oxygen không thay đổi nhiều.

Bài 5 trang 25 Toán 12 Tập 1: Tìm tiệm cận của đồ thị hàm số khối lượng hạt $m=m\left(v\right)=\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}$ trong hoạt động khởi động (trang 19).

Lời giải:

Tập xác định: D = (0; c].

Có $\underset{v\to c^{+}}{\lim }m\left(v\right)=\underset{v\to c^{+}}{\lim }\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}=+\infty ;$ $\underset{v\to c^{-}}{\lim }m\left(v\right)=\underset{v\to c^{-}}{\lim }\frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}}=+\infty$

Do đó v = c là tiệm cận đứng của đồ thị hàm số.

Hàm số không có tiệm cận ngang.

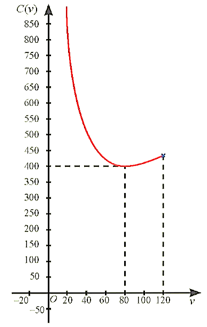
Hoạt động khởi động trang 25 Toán 12 Tập 1: Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức:

$C\left(v\right)=\frac{16000}{v}+\frac{5}{2}v\left(0<v\le 120\right)$

Để biểu diễn trực quan sự thay đổi của C(v) theo v, người ta đã vẽ đồ thị hàm số C = C(v) như hình bên. Làm thế nào để vẽ được đồ thị hàm số này?

Lời giải:

Sau bài học này, ta khảo sát và vẽ đồ thị của hàm số C = C(v).

– Tập xác định: D = (0; 120].

– Sự biến thiên:

+ Chiều biến thiên:

● Đạo hàm C'(v) = $-\frac{16000}{v^2}+\frac{5}{2}=\frac{5\left(v-80\right)\left(v+80\right)}{2v^2}$;

C'(v) = 0 ⇔ v = – 80 (loại) hoặc v = 80.

● Trên khoảng (0; 80), C'(v) < 0 nên hàm số nghịch biến trên khoảng này.

● Trên khoảng (80; 120), C'(v) > 0 nên hàm số đồng biến trên khoảng này.

+ Cực trị: Hàm số đạt cực tiểu tại v = 80, C_CT = C(80) = 400.

+ Giới hạn vô cực và tiệm cận: $\underset{v\to 0^{+}}{\lim }C\left(v\right)=\underset{v\to 0^{+}}{\lim }\left(\frac{16000}{v}+\frac{5}{2}v\right)=+\infty$ nên đường thẳng v = 0 là tiệm cận đứng của đồ thị hàm số.

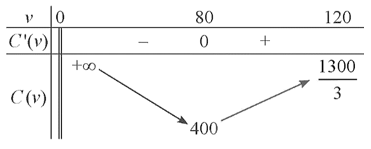
+ Bảng biến thiên:

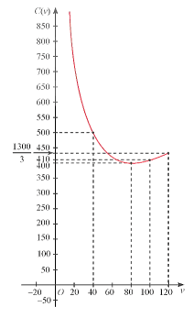
– Đồ thị:

Đồ thị hàm số có điểm cực tiểu (80; 400) và đi qua các điểm (40; 500), (100; 410), $\left(120;\frac{1300}{3}\right)$ như hình dưới đây.

Hoạt động khám phá trang 25 Toán 12 Tập 1: Cho hàm số y = – x² + 4x – 3.

a) Lập bảng biến thiên.

b) Vẽ đồ thị của hàm số.

Lời giải:

a) Xét hàm số y = – x² + 4x – 3.

Tập xác định: D = ℝ.

Ta có y' = – 2x + 4;

          y' = 0 ⇔ – 2x + 4 = 0 ⇔ x = 2.

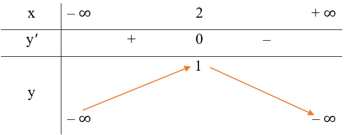
Bảng biến thiên:

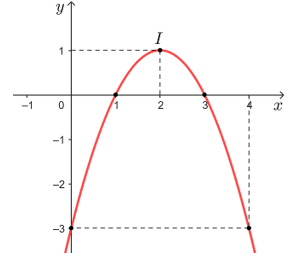
b) Hàm số đã cho là hàm số bậc hai có hệ số a = – 1 nên đồ thị hàm số là một parabol có bề lõm hướng xuống dưới, có đỉnh I(2; 1), đi qua các điểm (0; – 3), (1; 0), (3; 0) và (4; – 3).

Ta vẽ được đồ thị hàm số như sau:

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay khác:

• Giải Toán 12 trang 19
• Giải Toán 12 trang 21
• Giải Toán 12 trang 24