Bài 4.18 trang 26 Toán 12 Tập 2 - Kết nối tri thức

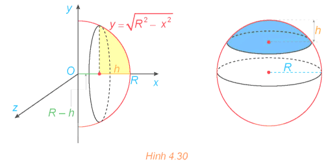
Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình , trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.

Giải Toán 12 Bài 13: Ứng dụng hình học của tích phân - Kết nối tri thức

Bài 4.18 trang 26 Toán 12 Tập 2: Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình $y=\sqrt{R^2-x^2}$, trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.

Lời giải:

Thể tích cần tìm là:

$V=\pi \underset{R-h}{\overset{R}{\int }}\left(R^2-x^2\right)dx$$=\pi {\left.\left(R^{2}x-\frac{x^3}{3}\right)\right|}_{R-h}^R$

$=\pi \left(R^3-\frac{R^3}{3}-R^2\left(R-h\right)+\frac{{\left(R-h\right)}^3}{3}\right)$

$=\pi \left(R^3-\frac{R^3}{3}-R^3+R^{2}h+\frac{R^3}{3}-R^{2}h+R{h}^2-\frac{h^3}{3}\right)$

$=\pi \left(R{h}^2-\frac{h^3}{3}\right)$$=\pi h^2\left(R-\frac{h}{3}\right)$

Lời giải bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân hay, chi tiết khác:

• HĐ1 trang 19 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12) ....

• Luyện tập 1 trang 20 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi parabol y = x² – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15) ....

• HĐ2 trang 20 Toán 12 Tập 2: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x² + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16) ....

• Luyện tập 2 trang 21 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=\sqrt{x}$, y = x – 2 và hai đường thẳng x = 1, x = 4 ....

• Vận dụng 1 trang 22 Toán 12 Tập 2: Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm ....

• HĐ3 trang 22 Toán 12 Tập 2: Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20) ....

• Vận dụng 2 trang 23 Toán 12 Tập 2: Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S₀, S₁ và chiều cao bằng h (H.4.24) ....

• HĐ4 trang 24 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{2}x$, trục hoành và hai đường thẳng x = 0, x = 4 ....

• Vận dụng 3 trang 25 Toán 12 Tập 2: a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r ....

• Bài 4.14 trang 25 Toán 12 Tập 2: Tính diện tích của hình phẳng được tô màu trong Hình 4.29 ....

• Bài 4.15 trang 25 Toán 12 Tập 2: Tính diện tích của hình phẳng giới hạn bởi các đường ....

• Bài 4.16 trang 25 Toán 12 Tập 2: Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia ....

• Bài 4.17 trang 26 Toán 12 Tập 2: Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x², y = 0, x = 0, x = 2 ....

• Bài 4.19 trang 26 Toán 12 Tập 2: Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và $\widehat{AOB}=\alpha \left(0<\alpha \le \frac{\pi }{4}\right)$ ....