Vận dụng 2 trang 23 Toán 12 Tập 2 - Kết nối tri thức

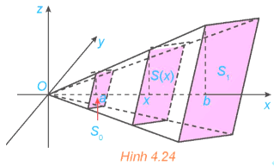
Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S, S và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Giải Toán 12 Bài 13: Ứng dụng hình học của tích phân - Kết nối tri thức

Vận dụng 2 trang 23 Toán 12 Tập 2: Tính thể tích của khối chóp cụt đều có diện tích hai đáy là S₀, S₁ và chiều cao bằng h (H.4.24). Từ đó suy ra công thức tính thể tích khối chóp đều có diện tích đáy bằng S và chiều cao bằng h.

Lời giải:

Chọn hệ trục tọa độ Oxyz như hình vẽ.

Gọi a, b lần lượt là khoảng cách từ O đến đáy nhỏ và đáy lớn của hình chóp. Khi đó chiều cao của hình chóp cụt là h = b – a.

Thiết diện của khối chóp cụt khi cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x (a ≤ x ≤ b) là một đa giác đều đồng dạng với đáy lớn của hình chóp cụt theo tỉ số đồng dạng là $\frac{x}{b}$

Khi đó $\frac{S\left(x\right)}{S_1}=\frac{x^2}{b^2}\Rightarrow S\left(x\right)=\frac{x^2}{b^2}.S_1$

Do đó thể tích khối chóp cụt đều là:

$V=\underset{a}{\overset{b}{\int }}S\left(x\right)dx=\underset{a}{\overset{b}{\int }}\frac{x^2}{b^2}{S}_{1}dx={\left.\frac{S_1}{b^2}.\frac{x^3}{3}\right|}_a^b$$=\frac{S_1}{3b^2}\left(b^3-a^3\right)$

$=\frac{b-a}{3b^2}.\left(S_1{b}^2+S_{1}ab+S_1{a}^2\right)$$=\frac{h}{3}.\left[S_1+S_1\frac{a}{b}+S_1{\left(\frac{a}{b}\right)}^2\right]$

Vì $\frac{S_0}{S_1}={\left(\frac{a}{b}\right)}^2\Rightarrow S_0=S_1.{\left(\frac{a}{b}\right)}^2$; $S_0{S}_1=S_1^2.{\left(\frac{a}{b}\right)}^2$$\Rightarrow \sqrt{S_0{S}_1}=S_1.\frac{a}{b}$

Do đó $V=\frac{h}{3}.\left[S_1+\sqrt{S_1.S_0}+S_0\right]$

Khối chóp đều được coi là khối chóp cụt đều khi S₀ = 0.

Do đó thể tích khối chóp đều là $V=\frac{1}{3}.S.h$

Lời giải bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân hay, chi tiết khác:

• HĐ1 trang 19 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đường thẳng y = f(x) = x + 1, trục hoành và hai đường thẳng x = −2; x = 1 (H.4.12) ....

• Luyện tập 1 trang 20 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi parabol y = x² – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15) ....

• HĐ2 trang 20 Toán 12 Tập 2: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x² + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16) ....

• Luyện tập 2 trang 21 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số $y=\sqrt{x}$, y = x – 2 và hai đường thẳng x = 1, x = 4 ....

• Vận dụng 1 trang 22 Toán 12 Tập 2: Ta biết rằng hàm cầu liên quan đến giá p của một sản phẩm với nhu cầu của người tiêu dùng, hàm cung liên quan đến giá p của sản phẩm ....

• HĐ3 trang 22 Toán 12 Tập 2: Xét hình trụ có bán kính đáy R, có trục là trục hoành Ox, nằm giữa hai mặt phẳng x = a và x = b (a < b) (H.4.20) ....

• HĐ4 trang 24 Toán 12 Tập 2: Xét hình phẳng giới hạn bởi đồ thị hàm số $f\left(x\right)=\frac{1}{2}x$, trục hoành và hai đường thẳng x = 0, x = 4 ....

• Vận dụng 3 trang 25 Toán 12 Tập 2: a) Tính thể tích của khối tròn xoay sinh ra khi quay hình thang vuông OABC trong mặt phẳng Oxy với OA = h, AB = R và OC = r ....

• Bài 4.14 trang 25 Toán 12 Tập 2: Tính diện tích của hình phẳng được tô màu trong Hình 4.29 ....

• Bài 4.15 trang 25 Toán 12 Tập 2: Tính diện tích của hình phẳng giới hạn bởi các đường ....

• Bài 4.16 trang 25 Toán 12 Tập 2: Các nhà kinh tế sử dụng đường cong Lorenz để minh họa sự phân phối thu nhập trong một quốc gia. Gọi x là đại diện cho phần trăm số gia đình trong một quốc gia ....

• Bài 4.17 trang 26 Toán 12 Tập 2: Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x², y = 0, x = 0, x = 2 ....

• Bài 4.18 trang 26 Toán 12 Tập 2: Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình $y=\sqrt{R^2-x^2}$ ....

• Bài 4.19 trang 26 Toán 12 Tập 2: Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và $\widehat{AOB}=\alpha \left(0<\alpha \le \frac{\pi }{4}\right)$ ....