HĐ3 trang 23 Toán 12 Tập 1 - Kết nối tri thức

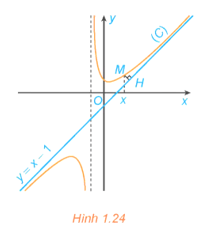
Cho hàm số có đồ thị (C) và đường thẳng y = x −1 như hình 1.24.

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số - Kết nối tri thức

HĐ3 trang 23 Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=x-1+\frac{2}{x+1}$ có đồ thị (C) và đường thẳng y = x −1 như hình 1.24.

a) Với x > −1, xét điểm M(x; f(x)) thuộc (C). Gọi H là hình chiếu vuông góc của M trên đường thẳng y = x – 1. Có nhận xét gì về khoảng cách MH khi x → +∞?

b) Chứng tỏ rằng $\underset{x\to +\infty }{\lim }\left[f\left(x\right)-\left(x-1\right)\right]=0$. Tính chất này thể hiện trên Hình 1.24 như thế nào?

Lời giải:

a) Ta có y = x – 1 ⇔ x – y – 1 = 0 (d).

Khi đó $MH=d(M,d)=\frac{\left|x-f\left(x\right)-1\right|}{\sqrt{2}}=\frac{\left|x-1-\left(x-1+\frac{2}{x+1}\right)\right|}{\sqrt{2}}=\frac{\sqrt{2}}{x+1}$(vì x > −1).

Ta có $\underset{x\to +\infty }{\lim }\frac{\sqrt{2}}{x+1}=0$.

Vậy MH sẽ dần tới 0 khi x → +∞.

b) Ta có $\underset{x\to +\infty }{\lim }\left[x-1+\frac{2}{x+1}-\left(x-1\right)\right]=\underset{x\to +\infty }{\lim }\frac{2}{x+1}=0$.

Khi x tiến đến vô cùng, đồ thị của hàm số f(x) và đường thẳng y = x – 1 tiến gần nhau và hình chiếu vuông góc của M lên đường thẳng này cũng gần đến đường thẳng y = x – 1.

Lời giải bài tập Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số hay, chi tiết khác:

• Mở đầu trang 20 Toán 12 Tập 1: Giả sử khối lượng còn lại của một chất phóng xạ (gam) sau t ngày phân rã được cho bởi hàm số ....

• HĐ1 trang 20 Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=\frac{2x+1}{x}$ có đồ thị (C). Với x > 0, xét điểm M(x; f(x)) thuộc (C) ....

• Luyện tập 1 trang 21 Toán 12 Tập 1: Tìm tiệm cận ngang của đồ thị hàm số $y=f\left(x\right)=\frac{2x-1}{x-1}$. ....

• Vận dụng 1 trang 21 Toán 12 Tập 1: Giải bài toán trong tình huống mở đầu ....

• HĐ2 trang 21 Toán 12 Tập 1: Cho hàm số $y=f\left(x\right)=\frac{x}{x-1}$ có đồ thị (C). Với x > 1, xét điểm M(x; f(x)) thuộc (C) ....

• Luyện tập 2 trang 22 Toán 12 Tập 1: Tìm các tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=f\left(x\right)=\frac{2x+1}{x-4}$ ....

• Vận dụng 2 trang 22 Toán 12 Tập 1: Để loại bỏ p% một loài tảo độc khỏi một hồ nước, người ta ước tính chi phí bỏ ra là $C\left(p\right)=\frac{45p}{100-p}$ ....

• Luyện tập 3 trang 24 Toán 12 Tập 1: Tìm các tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y=f\left(x\right)=\frac{x^2-4x+2}{1-x}$ ....

• Bài 1.16 trang 25 Toán 12 Tập 1: Hình 1.26 là đồ thị của hàm số $y=f\left(x\right)=\frac{2x^2}{x^2-1}$. Sử dụng đồ thị này, hãy ....

• Bài 1.17 trang 25 Toán 12 Tập 1: Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số $y=\frac{x^2+2x-3}{x-1}$ không? ....

• Bài 1.18 trang 25 Toán 12 Tập 1: Tìm các tiệm cận của đồ thị các hàm số sau: ....

• Bài 1.19 trang 25 Toán 12 Tập 1: Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là C(x) = 2x + 50 (triệu đồng) ....

• Bài 1.20 trang 25 Toán 12 Tập 1: Một mảnh vườn hình chữ nhật có diện tích bằng 144 m². Biết độ dài một cạnh của mảnh vườn là x (m) ....