Giải Toán 12 trang 20 Tập 2 Kết nối tri thức

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 20 Tập 2 trong Bài 13: Ứng dụng hình học của tích phân Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 20.

Giải Toán 12 trang 20 Tập 2 Kết nối tri thức

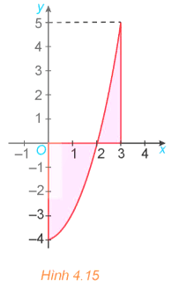
Luyện tập 1 trang 20 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi parabol y = x² – 4, trục hoành và hai đường thẳng x = 0; x = 3 (H.4.15).

Lời giải:

Diện tích hình phẳng cần tính là:

$\underset{0}{\overset{3}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left|x^2-4\right|dx+\underset{2}{\overset{3}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left(4-x^2\right)dx+\underset{2}{\overset{3}{\int }}\left(x^2-4\right)dx$

$={\left.\left(4x-\frac{x^3}{3}\right)\right|}_0^2+{\left.\left(\frac{x^3}{3}-4x\right)\right|}_2^3$$=\frac{16}{3}-3+\frac{16}{3}=\frac{23}{3}$

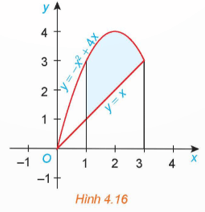
HĐ2 trang 20 Toán 12 Tập 2: Gọi S là diện tích hình phẳng giới hạn bởi đồ thị của các hàm số f(x) = −x² + 4x, g(x) = x và hai đường thẳng x = 1, x = 3 (H.4.16).

a) Giả sử S₁ là diện tích hình phẳng giới hạn bởi parabol y = −x² + 4x, trục hoành và hai đường thẳng x = 1, x = 3; S₂ là diện tích hình phẳng giới hạn bởi đường thẳng y = x, trục hoành và hai đường thẳng x = 1, x = 3. Tính S₁, S₂ và từ đó suy ra S.

b) Tính $\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$ và so sánh với S.

Lời giải:

a) Ta có $S_1=\underset{1}{\overset{3}{\int }}\left|-x^2+4x\right|dx$$=\underset{1}{\overset{3}{\int }}\left(-x^2+4x\right)dx$$={\left.\left(-\frac{x^3}{3}+2x^2\right)\right|}_1^3$$=9-\frac{5}{3}=\frac{22}{3}$

$S_2=\underset{1}{\overset{3}{\int }}\left|x\right|dx$$=\underset{1}{\overset{3}{\int }}xdx$$={\left.\frac{x^2}{2}\right|}_1^3=\frac{9}{2}-\frac{1}{2}=4$

Do đó S = S₁ – S₂ = $\frac{22}{3}-4=\frac{10}{3}$

b) $\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$$=\underset{1}{\overset{3}{\int }}\left|-x^2+4x-x\right|dx$$=\underset{1}{\overset{3}{\int }}\left|-x^2+3x\right|dx$

$=\underset{1}{\overset{3}{\int }}\left(-x^2+3x\right)dx$$={\left.\left(-\frac{x^3}{3}+3.\frac{x^2}{2}\right)\right|}_1^3$$=\frac{9}{2}-\frac{7}{6}=\frac{10}{3}$

Vậy $S=\underset{1}{\overset{3}{\int }}\left|f\left(x\right)-g\left(x\right)\right|dx$

Lời giải bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân hay khác:

• Giải Toán 12 trang 22
• Giải Toán 12 trang 25
• Giải Toán 12 trang 26