Giải Toán 12 trang 26 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 26 Tập 2 trong Bài 13: Ứng dụng hình học của tích phân Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 26.

Giải Toán 12 trang 26 Tập 2 Kết nối tri thức

Bài 4.17 trang 26 Toán 12 Tập 2: Tính thể tích của khối tròn xoay sinh ra khi quay hình phẳng giới hạn bởi các đường sau xung quanh trục Ox: y = 2x – x², y = 0, x = 0, x = 2.

Lời giải:

Thể tích cần tìm là:

$V=\pi \underset{0}{\overset{2}{\int }}{\left(2x-x^2\right)}^{2}dx$$=\pi \underset{0}{\overset{2}{\int }}\left(4x^2-4x^3+x^4\right)dx$$=\pi {\left.\left(\frac{4}{3}{x}^3-x^4+\frac{x^5}{5}\right)\right|}_0^2$$=\frac{16\pi }{15}$

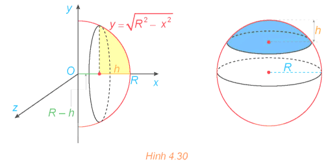
Bài 4.18 trang 26 Toán 12 Tập 2: Khối chỏm cầu có bán kính R và chiều cao h (0 < h ≤ R) sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình $y=\sqrt{R^2-x^2}$, trục hoành và hai đường thẳng x = R – h, x = R xung quanh trục Ox (H.4.30). Tính thể tích của khối chỏm cầu này.

Lời giải:

Thể tích cần tìm là:

$V=\pi \underset{R-h}{\overset{R}{\int }}\left(R^2-x^2\right)dx$$=\pi {\left.\left(R^{2}x-\frac{x^3}{3}\right)\right|}_{R-h}^R$

$=\pi \left(R^3-\frac{R^3}{3}-R^2\left(R-h\right)+\frac{{\left(R-h\right)}^3}{3}\right)$

$=\pi \left(R^3-\frac{R^3}{3}-R^3+R^{2}h+\frac{R^3}{3}-R^{2}h+R{h}^2-\frac{h^3}{3}\right)$

$=\pi \left(R{h}^2-\frac{h^3}{3}\right)$$=\pi h^2\left(R-\frac{h}{3}\right)$

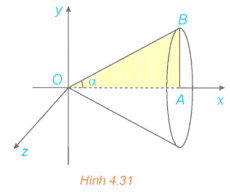
Bài 4.19 trang 26 Toán 12 Tập 2: Cho tam giác vuông OAB có cạnh OA = a nằm trên trục Ox và $\widehat{AOB}=\alpha \left(0<\alpha \le \frac{\pi }{4}\right)$. Gọi β là khối tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox (H.4.31).

a) Tính thể tích V của β theo a và α.

b) Tìm α sao cho thể tích V lớn nhất

Lời giải:

a) Xét tam giác OAB vuông tại A, có AB = OA.tanα = a.tanα.

Khi quay miền tam giác OAB xung quanh trục Ox ta được khối nón có bán kính đáy r = AB = a.tanα và chiều cao h = OA = a.

Do đó $V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi a^3{\tan }^2\alpha$

b) Có $V^{\text{'}}=\frac{1}{3}\pi a^3.2\tan \alpha .\frac{1}{{\cos }^2\alpha }$

Vì $0<\alpha \le \frac{\pi }{4}$ => 0 < tanα ≤ 1 nên V' > 0. Do đó V là hàm số đồng biến trên $\left(0;\frac{\pi }{4}\right)$

Do đó $\underset{\left(0;\frac{\pi }{4}\right]}{\max }V=V\left(\frac{\pi }{4}\right)=\frac{1}{3}\pi a^3$

Vậy $\alpha =\frac{\pi }{4}$ thì thể tích khối nón là lớn nhất.

Lời giải bài tập Toán 12 Bài 13: Ứng dụng hình học của tích phân hay khác:

• Giải Toán 12 trang 20
• Giải Toán 12 trang 22
• Giải Toán 12 trang 25