Giải Toán 12 trang 27 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 27 Tập 2 trong Bài tập cuối chương 4 Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 27.

Giải Toán 12 trang 27 Tập 2 Kết nối tri thức

Bài 4.20 trang 27 Toán 12 Tập 2: Một nguyên hàm của hàm số f(x) = sin2x là:

A. F(x) = 2cos2x.

B. F(x) = −cos2x.

C. $F\left(x\right)=\frac{1}{2}\cos 2x$

D. $F\left(x\right)=\frac{-1}{2}\cos 2x$

Lời giải:

Đáp án đúng là: D

Vì $F^{\text{'}}\left(x\right)={\left(\frac{-1}{2}\cos 2x\right)}^{\text{'}}=\sin 2x$ nên $F\left(x\right)=\frac{-1}{2}\cos 2x$ là một nguyên hàm của hàm số f(x) = sin2x.

Bài 4.21 trang 27 Toán 12 Tập 2: Họ tất cả các nguyên hàm của hàm số 2ex là

A. 2xe^x + C.

B. −2e^x + C.

C. 2e^x.

D. 2e^x + C.

Lời giải:

Đáp án đúng là: D

Có $\int 2e^{x}dx=2\int e^{x}dx=2e^x+C$

Bài 4.22 trang 27 Toán 12 Tập 2: Nguyên hàm F(x) của hàm số f(x) = e^x – 3e^−x thỏa mãn F(0) = 4 là

A. F(x) = e^x – 3e^−x.

B. F(x) = e^x + 3e^−2x.

C. F(x) = e^x + 3e^−x.

D. F(x) = e^x + 3e^−x + 4.

Lời giải:

Đáp án đúng là: C

Ta có $F\left(x\right)=\int \left(e^x-3e^{-x}\right)dx=e^x+3e^{-x}+C$

Vì F(0) = 4 nên e⁰ + 3e⁻⁰ + C = 4 Þ C = 0.

Vậy F(x) = e^x + 3e^−x.

Bài 4.23 trang 27 Toán 12 Tập 2: Cho hàm số f(x) có đạo hàm f'(x) liên tục trên ℝ, f(1) = 16 và $\underset{1}{\overset{3}{\int }}{f}^{\text{'}}\left(x\right)dx=4$. Khi đó giá trị của f(3) bằng

A. 20.

B. 16.

C. 12.

D. 10.

Lời giải:

Đáp án đúng là: A

Có $\underset{1}{\overset{3}{\int }}{f}^{\text{'}}\left(x\right)dx=4$$\iff {\left.f\left(x\right)\right|}_1^3=4$$\iff f\left(3\right)-f\left(1\right)=4\Rightarrow f\left(3\right)=4+f\left(1\right)=4+16=20$

Bài 4.24 trang 27 Toán 12 Tập 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x² – 2x, y = −x² + 4x và hai đường thẳng x = 0, x = 3 là

A. −9.

B. 9.

C. $\frac{16}{3}$

D. $\frac{20}{3}$

Lời giải:

Đáp án đúng là: B

Diện tích cần tìm là:

$S=\underset{0}{\overset{3}{\int }}\left|x^2-2x+x^2-4x\right|dx$$=\underset{0}{\overset{3}{\int }}\left|2x^2-6x\right|dx$$=\underset{0}{\overset{3}{\int }}\left(6x-2x^2\right)dx$

$={\left.\left(3x^2-\frac{2}{3}{x}^3\right)\right|}_0^3$

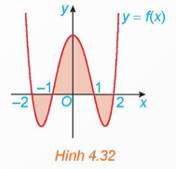
Bài 4.25 trang 27 Toán 12 Tập 2: Cho đồ thị hàm số y = f(x) trên đoạn [−2;2] như Hình 4.32.

Biết $\underset{-2}{\overset{-1}{\int }}f\left(x\right)dx=\underset{1}{\overset{2}{\int }}f\left(x\right)dx=-\frac{22}{15}$ và $\underset{-1}{\overset{1}{\int }}f\left(x\right)dx=\frac{76}{15}$. Khi đó, diện tích của hình phẳng được tô màu là

A. 8.

B. $\frac{22}{15}$

C. $\frac{32}{15}$

D. $\frac{76}{15}$

Lời giải:

Đáp án đúng là: A

Diện tích cần tìm là:

$S=\underset{-2}{\overset{2}{\int }}\left|f\left(x\right)\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|f\left(x\right)\right|dx+\underset{-1}{\overset{1}{\int }}\left|f\left(x\right)\right|dx+\underset{1}{\overset{2}{\int }}\left|f\left(x\right)\right|dx$

$=-\underset{-2}{\overset{-1}{\int }}f\left(x\right)dx+\underset{-1}{\overset{1}{\int }}f\left(x\right)dx-\underset{1}{\overset{2}{\int }}f\left(x\right)dx$

$=\frac{22}{15}+\frac{76}{15}+\frac{22}{15}=8$

Lời giải bài tập Toán 12 Bài tập cuối chương 4 hay khác:

• Giải Toán 12 trang 28