Giải Toán 12 trang 42 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 42 Tập 1 trong Bài tập cuối chương 1 Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 42.

Giải Toán 12 trang 42 Tập 1 Kết nối tri thức

Bài 1.30 trang 42 Toán 12 Tập 1: Cho hàm số y = f(x) có đạo hàm trên khoảng (a; b). Phát biểu nào dưới đây là đúng?

A. Nếu f'(x) ≥ 0 với mọi x thuộc (a; b) thì hàm số y = f(x) đồng biến trên (a; b).

B. Nếu f'(x) > 0 với mọi x thuộc (a; b) thì hàm số y = f(x) đồng biến trên (a; b).

C. Hàm số y = f(x) đồng biến trên (a; b) khi và chỉ khi f'(x) ≥ 0 với mọi x thuộc (a; b).

D. Hàm số y = f(x) đồng biến trên (a; b) khi và chỉ khi f'(x) > 0 với mọi x thuộc (a; b).

Lời giải:

Đáp án đúng là: B

Nếu f'(x) > 0 với mọi x thuộc (a; b) thì hàm số y = f(x) đồng biến trên (a; b).

Bài 1.31 trang 42 Toán 12 Tập 1: Hàm số nào sau đây nghịch biến trên ℝ.

A. y = −x³ + 3x² – 9x.                       B. y = −x³ + x + 1.

C. $y=\frac{x-1}{x-2}$                                     D. y = 2x² + 3x + 2.

Lời giải:

Đáp án đúng là: A

Xét hàm số y = −x³ + 3x² – 9x.

Có y' = −3x² +6x – 9 =−3(x² – 2x + 3) = −3(x −1)² – 6 < 0 với mọi x thuộc ℝ.

Do đó hàm số y = −x³ + 3x² – 9x nghịch biến trên ℝ.

Bài 1.32 trang 42 Toán 12 Tập 1: Hàm số nào dưới đây không có cực trị?

A. y = |x|.             B. y = x⁴.              C. y = −x³ + x.     D. $y=\frac{2x-1}{x+1}$.

Lời giải:

Đáp án đúng là: D

Xét hàm số $y=\frac{2x-1}{x+1}$

Có $y^{\text{'}}=\frac{2\left(x+1\right)-\left(2x-1\right)}{{\left(x+1\right)}^2}=\frac{3}{{\left(x+1\right)}^2}>\mathrm{0,}\forall x\ne -1$

Do đó hàm số $y=\frac{2x-1}{x+1}$ không có cực trị.

Bài 1.33 trang 42 Toán 12 Tập 1: Giá trị cực tiểu của hàm số y = x²lnx là

A. $\frac{1}{e}$.                    B. -$\frac{1}{e}$.                  C. -$\frac{1}{2e}$.                D. $\frac{1}{2e}$.

Lời giải:

Đáp án đúng là: C

Tập xác định là D = (0; +∞).

Có y' = 2xlnx + x = x(2lnx + 1).

Có y' = 0 $\iff 2\ln x+1=0\iff x=\frac{1}{\sqrt{e}}$ (do x > 0).

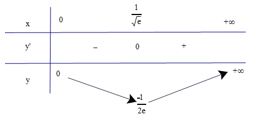
Bảng biến thiên

Dựa vào bảng biến thiên ta có giá trị cực tiểu của hàm số là $-\frac{1}{2e}$.

Bài 1.34 trang 42 Toán 12 Tập 1: Giá trị lớn nhất của hàm số y = (x – 2)²e^x trên đoạn [1; 3] là

A. 0.                     B. e³.                    C. e⁴.                    D. e.

Lời giải:

Đáp án đúng là: B

Có y' = 2(x – 2)e^x + (x – 2)²e^x = x(x – 2)e^x.

Có y' = 0 ⇔ x(x – 2) = 0 ⇔ x = 0 (loại) hoặc x = 2 (thỏa mãn).

Có y(1) = e; y(2) = 0; y(3) = e³.

Vậy giá trị lớn nhất của hàm số là e³ khi x = 3.

Bài 1.35 trang 42 Toán 12 Tập 1: Cho hàm số y = f(x) thỏa mãn: $\underset{x\to 2^{+}}{\lim }f\left(x\right)=1;\underset{x\to 2^{-}}{\lim }f\left(x\right)=1;\underset{x\to -\infty }{\lim }f\left(x\right)=2$ và $\underset{x\to +\infty }{\lim }f\left(x\right)=2$. Khẳng định nào sau đây là đúng?

A. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.

B. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

C. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số.

D. Đường thẳng x = 2 là tiệm cận ngang của đồ thị hàm số.

Lời giải:

Đáp án đúng là: B

Vì $\underset{x\to -\infty }{\lim }f\left(x\right)=2$ và $\underset{x\to +\infty }{\lim }f\left(x\right)=2$ nên đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số.

$\underset{x\to 2^{+}}{\lim }f\left(x\right)=1;\underset{x\to 2^{-}}{\lim }f\left(x\right)=1$ nên đồ thị hàm số không có tiệm cận đứng.

Bài 1.36 trang 42 Toán 12 Tập 1: Tiệm cận xiên của đồ thị hàm số $y=\frac{x^2+2x-2}{x+2}$ là

A. y = −2.             B. y = 1.               C. y = x + 2.         D. y = x.

Lời giải:

Đáp án đúng là: D

Có $y=\frac{x^2+2x-2}{x+2}=x-\frac{2}{x+2}$

$\underset{x\to +\infty }{\lim }\left(y-x\right)=\underset{x\to +\infty }{\lim }\frac{-2}{x+2}=0; \underset{x\to -\infty }{\lim }\left(y-x\right)=\underset{x\to -\infty }{\lim }\frac{-2}{x+2}=0$

Do đó y = x là tiệm cận xiên của đồ thị hàm số.

Lời giải bài tập Toán 12 Bài tập cuối chương 1 hay khác:

• Giải Toán 12 trang 43
• Giải Toán 12 trang 44