Giải Toán 12 trang 78 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 78 Tập 2 trong Bài 19: Công thức xác suất toàn phần và công thức Bayes Toán 12 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 78.

Giải Toán 12 trang 78 Tập 2 Kết nối tri thức

Bài 6.8 trang 78 Toán 12 Tập 2: Có hai chuồng thỏ. Chuồng I có 5 con thỏ đen và 10 con thỏ trắng. Chuồng II có 7 con thỏ đen và 3 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 1 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 1 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.

Lời giải:

Gọi A là biến cố: “Bắt được thỏ trắng từ chuồng II”;

       B là biến cố: “Sau đó bắt được thỏ trắng từ chuồng I”.

Ta cần tính P(B). Theo công thức xác suất toàn phần, ta có:

P(B) = P(A) ∙ P(B | A) + $P\left(\overline{A}\right)$. $P\left(B|\overline{A}\right)$

Vì chuồng II có 7 con thỏ đen và 3 con thỏ trắng nên ta có: $P\left(A\right)=\frac{3}{10}$.

Suy ra $P\left(\overline{A}\right)=1-P\left(A\right)=1-\frac{3}{10}=\frac{7}{10}$.

Nếu A xảy ra tức là bắt được thỏ trắng từ chuồng II rồi cho vào chuồng I thì chuồng I có 5 thỏ đen và 11 thỏ trắng. Do đó, $P\left(B|A\right)=\frac{11}{16}$.

Nếu A không xảy ra thì chuồng I có 6 thỏ đen và 10 thỏ trắng. Do đó, $P\left(B|\overline{A}\right)=\frac{10}{16}$.

Khi đó, P(B) = P(A) ∙ P(B | A) + $P\left(\overline{A}\right)$ . $P\left(B|\overline{A}\right)$$=\frac{3}{10}\cdot \frac{11}{16}+\frac{7}{10}\cdot \frac{10}{16}=\frac{103}{160}$.

Vậy xác suất để con thỏ được lấy ra là con thỏ trắng là

Bài 6.9 trang 78 Toán 12 Tập 2: Tại nhà máy X sản xuất linh kiện điện tử tỉ lệ sản phẩm đạt tiêu chuẩn là 80%. Trước khi xuất xưởng ra thị trường, các linh kiện điện tử đều phải qua khâu kiểm tra chất lượng để đóng dấu OTK. Vì sự kiểm tra không tuyệt đối hoàn hảo nên nếu một linh kiện điện tử đạt tiêu chuẩn thì nó có xác suất 0,99 được đóng dấu OTK; nếu một linh kiện điện tử không đạt tiêu chuẩn thì nó có xác suất 0,95 không được đóng dấu OTK. Chọn ngẫu nhiên một linh kiện điện tử của nhà máy X trên thị trường.

a) Tính xác suất để linh kiện điện tử đó được đóng dấu OTK.

b) Dùng sơ đồ hình cây, hãy mô tả cách tính xác suất để linh kiện điện tử được chọn không được đóng dấu OTK.

Lời giải:

a) Gọi A là biến cố: “Linh kiện điện tử được chọn đạt tiêu chuẩn”;

            B là biến cố: “Linh kiện điện tử được chọn được đóng dấu OTK”.

Ta cần tính P(B). Theo công thức xác suất toàn phần ta có:

P(B) = P(A) ∙ P(B | A) + $P\left(\overline{A}\right)$.$P\left(B|\overline{A}\right)$

Theo giả thiết P(A) = 0,8. Suy ra $P\left(\overline{A}\right)$ = 1 – P(A) = 1 – 0,8 = 0,2.

Tính P(B | A): Đây là xác suất để linh kiện điện tử đạt tiêu chuẩn được đóng dấu OTK. Theo giả thiết ta có P(B | A) = 0,99.

Tính $P\left(B|\overline{A}\right)$: Đây là xác suất để linh kiện điện tử không đạt tiêu chuẩn được đóng dấu OTK. Theo giả thiết nếu linh kiện điện tử không đạt tiêu chuẩn thì nó không được đóng dấu OTK với xác suất 0,95. Vậy nếu linh kiện điện tử không đạt tiêu chuẩn thì nó được đóng dấu OTK với xác suất là 1 – 0,95 = 0,05. Do đó $P\left(B|\overline{A}\right)$ = 0,05.

Khi đó, P(B) = P(A) ∙ P(B | A) + $P\left(\overline{A}\right)$ .$P\left(B|\overline{A}\right)$ = 0,8 ∙ 0,99 + 0,2 ∙ 0,05 = 0,802.

Vậy xác suất để linh kiện điện tử đó được đóng dấu OTK là 0,802.

b) Với A là biến cố: “Linh kiện điện tử được chọn đạt tiêu chuẩn”;

            B là biến cố: “Linh kiện điện tử được chọn được đóng dấu OTK”.

Khi đó, $\overline{B}$ là biến cố: “Linh kiện điện tử được chọn không được đóng dấu OTK”.

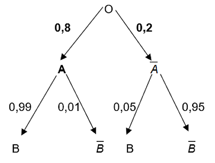
Ta vẽ sơ đồ hình cây như sau:

Có hai nhánh cây đi tới $\overline{B}$ là $OA\overline{B}$ và $O\overline{A}\overline{B}$.

Vậy $P\left(\overline{B}\right)$ = 0,8 ∙ 0,01 + 0,2 ∙ 0,95 = 0,198

Bài 6.10 trang 78 Toán 12 Tập 2: Có hai đội thi đấu môn Bắn súng. Đội I có 5 vận động viên, đội II có 7 vận động viên. Xác suất đạt huy chương vàng của mỗi vận động viên đội I và đội II tương ứng là 0,65 và 0,55. Chọn ngẫu nhiên một vận động viên.

a) Tính xác suất để vận động viên này đạt huy chương vàng;

b) Giả sử vận động viên được chọn đạt huy chương vàng. Tính xác suất để vận động viên này thuộc đội I.

Lời giải:

a) Gọi A là biến cố: “VĐV được chọn thuộc đội I”;

B là biến cố: “VĐV được chọn thuộc đội II”;

E là biến cố: “VĐV được chọn đạt HCV”.

(Với VĐV: vận động viên, HCV: huy chương vàng).

Ta có B = $\overline{A}$.

Ta cần tính P(E). Theo công thức xác suất toàn phần, ta có

P(E) = P(A) ∙ P(E | A) + $P\left(\overline{A}\right)$.$P\left(E|\overline{A}\right)$.

Theo bài ra ta có: $P\left(A\right)=\frac{5}{12}$, $P\left(\overline{A}\right)=P\left(B\right)=\frac{7}{12}$.

P(E | A) là xác suất để VĐV thuộc đội I đoạt HCV. Theo bài ra ta có P(E | A) = 0,65.

$P\left(E|\overline{A}\right)$ là xác suất để VĐV thuộc đội II đoạt HCV. Theo bài ra ta có $P\left(E|\overline{A}\right)$ = 0,55.

Thay vào ta được P(E) = $\frac{5}{12}\cdot \mathrm{0,65}+\frac{7}{12}\cdot \mathrm{0,55}\approx$0,5917.

Vậy xác suất để vận động viên này đạt huy chương vàng là khoảng 0,5917.

b) Ta có xác suất để vận động viên được chọn thuộc đội I, biết rằng vận động viên này đạt huy chương vàng, chính là xác suất P(A | E).

Theo công thức Bayes và kết quả ở câu a) ta có

$P\left(A|E\right)=\frac{P\left(A\right)\cdot P\left(E|A\right)}{P\left(E\right)}\approx \frac{\frac{5}{12}\cdot \mathrm{0,65}}{\mathrm{0,5917}}\approx \mathrm{0,4577}$

Bài 6.11 trang 78 Toán 12 Tập 2: Một bộ lọc được sử dụng để chặn thư rác trong các tài khoản thư điện tử. Tuy nhiên, vì bộ lọc không tuyệt đối hoàn hảo nên một thư rác bị chặn với xác suất 0,95 và một thư đúng (không phải là thư rác) bị chặn với xác suất 0,01. Thống kê cho thấy tỉ lệ thư rác là 3%.

a) Chọn ngẫu nhiên một thư bị chặn. Tính xác suất để đó là thư rác.

b) Chọn ngẫu nhiên một thư không bị chặn. Tính xác suất để đó là thư đúng.

c) Trong số các thư bị chặn, có bao nhiêu phần trăm là thư đúng? Trong số các thư không bị chặn, có bao nhiêu phần trăm là thư rác?

Lời giải:

a) Gọi A là biến cố: “Thư được chọn là thư rác”;

B là biến cố: “Thư được chọn là bị chặn”.

Ta có P(A) = 3% = 0,03; $P\left(\overline{A}\right)=1-P\left(A\right)=\mathrm{0,97}$ ; P(B | A) = 0,95; $P\left(B|\overline{A}\right)=\mathrm{0,01}$.

Ta cần phải tính P(A | B). Áp dụng công thức Bayes, ta có:

$P\left(A|B\right)=\frac{P\left(A\right)\cdot P\left(B|A\right)}{P\left(A\right)\cdot P\left(B|A\right)+P\left(\overline{A}\right)\cdot P\left(B|\overline{A}\right)}=\frac{\mathrm{0,03}\cdot \mathrm{0,95}}{\mathrm{0,03}\cdot \mathrm{0,95}+\mathrm{0,97}\cdot \mathrm{0,01}}\approx \mathrm{0,746}$

Vậy khi chọn ngẫu nhiên một thư bị chặn thì xác suất để đó là thư rác khoảng 0,746.

b) Ta phải tính $P\left(\overline{A}|\overline{B}\right)$.

Ta có $P\left(B|\overline{A}\right)=\mathrm{0,01}\Rightarrow P\left(\overline{B}|\overline{A}\right)=\mathrm{0,99}$; $P\left(B|A\right)=\mathrm{0,95}\Rightarrow P\left(\overline{B}|A\right)=\mathrm{0,05}$.

Áp dụng công thức Bayes, ta có:

$P\left(\overline{A}|\overline{B}\right)=\frac{P\left(\overline{A}\right)\cdot P\left(\overline{B}|\overline{A}\right)}{P\left(\overline{A}\right)\cdot P\left(\overline{B}|\overline{A}\right)+P\left(A\right)\cdot P\left(\overline{B}|A\right)}=\frac{\mathrm{0,97}\cdot \mathrm{0,99}}{\mathrm{0,97}\cdot \mathrm{0,99}+\mathrm{0,03}\cdot \mathrm{0,05}}\approx \mathrm{0,998}$

Vậy khi ngẫu nhiên một thư không bị chặn thì xác suất để đó là thư đúng khoảng 0,998.

c) Từ câu a), ta thấy xác suất một thư là thư rác nếu biết rằng thư đó bị chặn là 0,746. Nghĩa là trong số các thư bị chặn có khoảng 74,6% thư rác.

Vậy trong số các thư bị chặn có 100% – 74,6% = 25,4% là thư đúng.

Từ câu b), ta thấy xác suất để đó là thư đúng nếu biết rằng thư đó không bị chặn là 0,998. Nghĩa là trong số các thư không bị chặn có khoảng 99,8% thư đúng.

Vậy trong số các thư không bị chặn có 100% – 99,8% = 0,2% là thư rác.

Lời giải bài tập Toán 12 Bài 19: Công thức xác suất toàn phần và công thức Bayes hay khác:

• Giải Toán 12 trang 74
• Giải Toán 12 trang 77