Giải Toán 7 trang 117 Tập 2 Cánh diều

Haylamdo biên soạn và sưu tầm giải Toán 7 trang 117 Tập 2 trong Bài 13: Tính chất ba đường cao của tam giác Toán 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 117.

Giải Toán 7 trang 117 Tập 2 Cánh diều

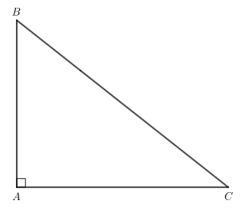
Luyện tập 1 trang 117 Toán lớp 7 Tập 2: Cho tam giác ABC vuông tại A. Hãy đọc tên đường cao đi qua B, đường cao đi qua C.

Lời giải:

Đường cao đi qua B và vuông góc với AC là AB.

Đường cao đi qua C và vuông góc với AB là AC.

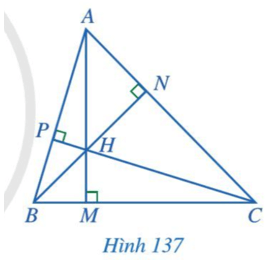
Hoạt động 2 trang 117 Toán lớp 7 Tập 2: Quan sát ba đường cao AM, BN, CP của tam giác ABC (Hình 137), cho biết ba đường cao đó có cùng đi qua một điểm hay không.

Lời giải:

Ta thấy ba đường cao AM, BN, CP của tam giác ABC cùng đi qua điểm H.

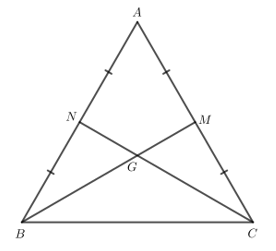
Luyện tập 2 trang 117 Toán lớp 7 Tập 2: Cho tam giác đều ABC có trọng tâm là G. Chứng minh G cũng là trực tâm của tam giác ABC.

Lời giải:

Gọi M, N theo thứ tự là trung điểm của AC và AB.

Do tam giác ABC đều nên AB = BC = CA và $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}$.

Do M là trung điểm của AC nên AM = CM.

Xét ∆BAM và ∆BCM có:

BA = BC (chứng minh trên).

$\widehat{BAM}=\widehat{BCM}$ (chứng minh trên).

AM = CM (chứng minh trên).

Do đó ∆BAM = ∆BCM (c - g - c).

Suy ra $\widehat{BMA}=\widehat{BMC}$ (2 góc tương ứng).

Mà $\widehat{BMA}+\widehat{BMC}=180°$ nên $\widehat{BMA}=\widehat{BMC}=90°$.

Do đó BM là đường cao của tam giác ABC.

Tương tự CN là đường cao của tam giác ABC.

Tam giác ABC có hai đường cao BM và CN cắt nhau tại G nên G là trực tâm của tam giác ABC.

Lời giải bài tập Toán lớp 7 Bài 13: Tính chất ba đường cao của tam giác Cánh diều hay khác:

• Giải Toán 7 trang 116 Tập 2

• Giải Toán 7 trang 118 Tập 2