Giải Toán 7 trang 88 Tập 2 Cánh diều

---

Haylamdo biên soạn và sưu tầm giải Toán 7 trang 88 Tập 2 trong Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc Toán 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 88.

Giải Toán 7 trang 88 Tập 2 Cánh diều

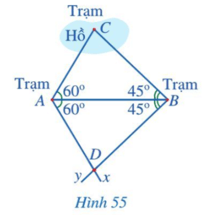
Khởi động trang 88 Toán lớp 7 Tập 2: Có ba trạm quan sát A, B, C trong đó trạm quan sát C ở giữa hồ.

Người ta muốn đo khoảng cách từ A và từ B đến C. Do không thể đo trực tiếp được các khoảng cách trên nên người ta làm như sau (Hình 55):

- Đo góc BAC được 60^o, đo góc ABC được 45^o;

- Kẻ tia Ax sao cho $\widehat{BAx}=60°$, kẻ tia By sao cho $\widehat{ABy}=45°$, xác định giao điểm D của hai tia đó;

- Đo khoảng cách AD và BD. Ta có AC = AD và BC = BD.

Tại sao lại có hai đẳng thức trên?

Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:

Lời giải:

Xét ∆ABC và ∆ABD có:

$\widehat{BAC}=\widehat{BA\text{D}}\left(=60°\right)$.

AB chung.

$\widehat{ABC}=\widehat{ABD}\left(=45°\right).$

Suy ra ∆ABC = ∆ABD (g - c - g).

Do đó AC = AD (2 cạnh tương ứng) và BC = BD (2 cạnh tương ứng).

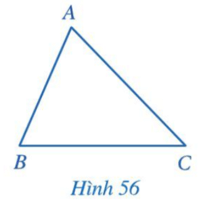
Hoạt động 1 trang 88 Toán lớp 7 Tập 2: Cho tam giác ABC (Hình 56).

Những góc nào của tam giác ABC có cạnh thuộc đường thẳng AB?

Trong tam giác ABC (Hình 56), ta gọi góc A và góc B là hai góc kề cạnh AB. Tương tự, góc B và góc C là hai góc kề cạnh BC, góc C và góc A là hai góc kề cạnh CA.

Lời giải:

Những góc của tam giác ABC có cạnh thuộc đường thẳng AB là: $\widehat{CAB}$ và $\widehat{CBA}$.

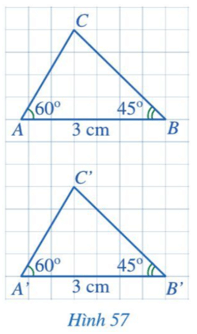
Hoạt động 2 trang 88 Toán lớp 7 Tập 2: Cho hai tam giác ABC và A’B’C’ (Hình 57) có: $\hat{A}=\widehat{A^{\text{'}}}=60°,$ AB = A’B’ = 3 cm, $\hat{B}=\widehat{B^{\text{'}}}=45°$.

Bằng cách đếm số ô vuông, hãy so sánh BC và B’C’. Từ đó có thể kết luận được hai tam giác ABC và A’B’C’ bằng nhau hay không?

Lời giải:

Dựa vào hình trên, bằng cách đếm số ô vuông, ta thấy BC = B’C’.

Từ đó ta có thể kết luận hai tam giác ABC và A’B’C’ bằng nhau bằng cách như sau:

Xét ∆ABC và ∆A'B'C' có:

AB = A’B’ (= 3cm).

$\widehat{ABC}=\widehat{A^{\text{'}}{B}^{\text{'}}{C}^{\text{'}}}\left(=45°\right)$.

BC = B’C’ (chứng minh trên).

Suy ra ∆ABC = ∆A'B'C' (c - g - c).

Vậy hai tam giác ABC và A’B’C’ bằng nhau.

Lời giải bài tập Toán lớp 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc Cánh diều hay khác:

• Giải Toán 7 trang 89 Tập 2

• Giải Toán 7 trang 91 Tập 2

• Giải Toán 7 trang 92 Tập 2