Bài 3 trang 78 Toán 7 Tập 2 Chân trời sáng tạo

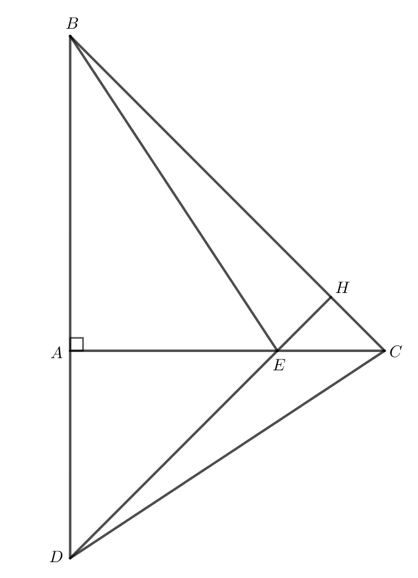
Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:

Giải Toán 7 Bài 8: Tính chất ba đường cao của tam giác - Chân trời sáng tạo

Bài 3 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:

a) DE vuông góc với BC;

b) BE vuông góc với DC.

Lời giải:

Gọi giao điểm của DE và BC là H.

Tam giác ABC vuông cân tại A nên $\widehat{ABC}+\widehat{ACB}=90°$(trong tam giác vuông, tổng hai góc nhọn bằng $90°$) và $\widehat{ABC}=\widehat{ACB}$.

Do đó $\widehat{ABC}=\widehat{ACB}=45°$.

Tam giác vuông ADE có AD = AE nên tam giác ADE vuông cân tại A.

Khi đó $\widehat{A\text{D}E}+\widehat{A\text{ED}}=90°$và $\widehat{A\text{D}E}=\widehat{A\text{ED}}$.

Do đó $\widehat{A\text{D}E}=\widehat{A\text{ED}}=45°$.

Ta có $\widehat{A\text{ED}}$là góc ngoài tại đỉnh E của tam giác EDC nên $\widehat{A\text{ED}}=\widehat{E\text{D}C}+\widehat{ECD}$.

Do đó $\widehat{E\text{D}C}+\widehat{ECD}=45°$.

Khi đó trong tam giác DHC:

$\widehat{DHC}=180°-\widehat{H\text{D}C}-\widehat{HC\text{D}}=180°-\widehat{H\text{D}C}-\widehat{EC\text{D}}-\widehat{ECH}$.

$\widehat{DHC}=180°-\left(\widehat{H\text{D}C}+\widehat{EC\text{D}}\right)-45°$.

$\widehat{DHC}=180°-45°-45°=90°$.

Do đó DH $\perp$BC.

b) Tam giác BDC có CA $\perp$BD, DH $\perp$BC nên CA, DH là hai đường cao của tam giác BDC.

Mà CA và DH cắt nhau tại E nên E là trực tâm của tam giác BDC.

Do đó BE vuông góc với DC.

Lời giải bài tập Toán 7 Bài 8: Tính chất ba đường cao của tam giác hay, chi tiết khác:

• Khởi động trang 77 Toán 7 Tập 2: Làm thế nào để tính khoảng cách từ mỗi đỉnh đến cạnh đối diện của một tam giác? ....

• Khám phá 1 trang 77 Toán 7 Tập 2: Em hãy vẽ một tam giác ABC trên giấy, sau đó dùng êke vẽ đoạn thẳng vuông góc từ đỉnh B ....

• Thực hành 1 trang 77 Toán 7 Tập 2: Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC. ....

• Vận dụng 1 trang 77 Toán 7 Tập 2: Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a). ....

• Khám phá 2 trang 77 Toán 7 Tập 2: Vẽ một tam giác rồi dùng êke vẽ ba đường cao của tam giác ấy (Hình 3). ....

• Thực hành 2 trang 78 Toán 7 Tập 2: Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6). ....

• Vận dụng 2 trang 78 Toán 7 Tập 2: Cho tam giác ABC có ba đường cao AD, BE, CF đồng quy tại trực tâm H. ....

• Bài 1 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB ....

• Bài 2 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. ....

• Bài 4 trang 78 Toán 7 Tập 2: Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều. ....