Giải Toán 7 trang 75 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 75 Tập 1 trong Bài 2: Tia phân giác Toán lớp 7 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 75.

Giải Toán 7 trang 75 Tập 1 Chân trời sáng tạo

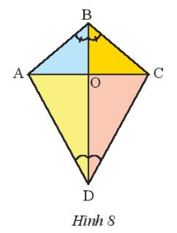
Bài 1 trang 75 Toán 7 Tập 1: a) Trong Hình 8, tìm tia phân giác của các góc $\widehat{ABC},\widehat{ADC}$.

b) Cho biết $\widehat{ABC}={100}^o$, $\widehat{ADC}={60}^o$. Tính số đo của các góc $\widehat{ABO},\widehat{ADO}$.

Lời giải:

a) Tia BO xuất phát từ đỉnh B của $\widehat{ABC}$, đi qua điểm O nằm trong $\widehat{ABC}$ và $\widehat{ABO}=\widehat{CBO}$.

Do đó, BO là tia phân giác của $\widehat{ABC}$.

Tia DO xuất phát từ đỉnh D của $\widehat{ADC}$, đi qua điểm B nằm trong $\widehat{ADC}$ và $\widehat{ADO}=\widehat{CDO}$.

Do đó, DO là tia phân giác của $\widehat{ADC}$.

Vậy BO và DO lần lượt là tia phân giác của các góc $\widehat{ABC},\widehat{ADC}$.

b) Vì BO là tia phân giác của $\widehat{ABC}$ nên:

$\widehat{ABO}=\widehat{CBO}=\frac{\widehat{ABC}}{2}=\frac{{100}^o}{2}={50}^o$.

Vì BO là tia phân giác của $\widehat{ABC}$ nên:

$\widehat{ADO}=\widehat{CDO}=\frac{\widehat{ADC}}{2}=\frac{{60}^o}{2}={30}^o$.

Vậy $\widehat{ABO}={50}^o$; $\widehat{ADO}={30}^o$.

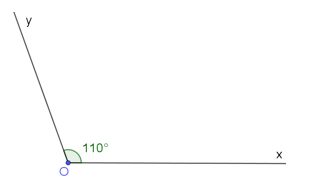
Bài 2 trang 75 Toán 7 Tập 1: a) Vẽ $\widehat{xOy}$ có số đo 110^o.

b) Vẽ tia phân giác của $\widehat{xOy}$ trong câu a.

Lời giải:

a) Các bước vẽ $\widehat{xOy}$ có số đo 110^o:

Bước 1: Vẽ tia Ox bất kì. Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh Ox của góc đi qua vạch 0 của thước và thước chồng lên phần trong của góc.

Bước 3: Tại vạch chỉ số 110 trên thước đo góc, chấm một chấm nhỏ. Nối điểm đó với điểm O.

Ta được $\widehat{xOy}$ có số đo 110^o.

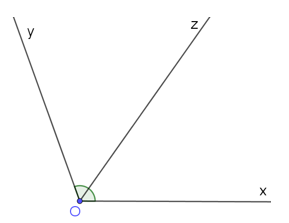
b) Giả sử Oz là tia phân giác của $\widehat{xOy}$ trong câu a.

Khi đó $\widehat{xOz}=\widehat{yOz}$ và $\widehat{xOz}+\widehat{yOz}={110}^o$.

Suy ra $\widehat{xOz}=\frac{\widehat{xOy}}{2}=\frac{{110}^o}{2}={55}^o$.

- Dùng thước đo góc vẽ tia Oz đi qua một điểm trong của $\widehat{xOy}$ sao cho $\widehat{xOz}={55}^o$.

Ta được tia Oz là phân giác của $\widehat{xOy}$.

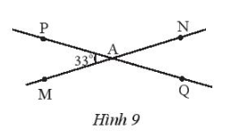
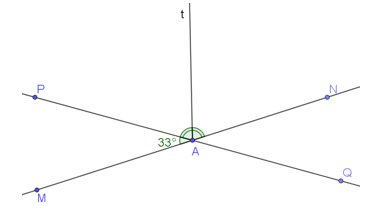
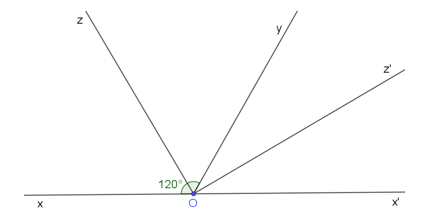
Bài 3 trang 75 Toán 7 Tập 1: Cho hai đường thẳng MN, PQ cắt nhau tại A và tạo thành $\widehat{PAM}={33}^o$ (Hình 9).

a) Tính số đo các góc còn lại.

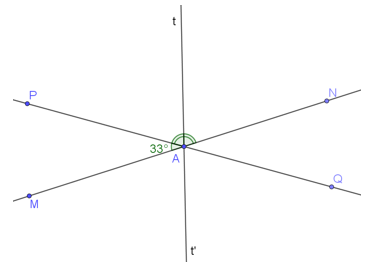
b) Vẽ At là tia phân giác của $\widehat{PAN}$. Hãy tính số đo của $\widehat{tAQ}$. Vẽ tia At’ là tia đối của tia At. Giải thích tại sao At’ là tia phân giác của $\widehat{MAQ}$.

Lời giải:

Thiếu số thứ tự ý a

a) Vì $\widehat{PAM}$ và $\widehat{PAN}$ là hai góc kề bù nên:

$\widehat{PAM}+\widehat{PAN}={180}^o$

${33}^o+\widehat{PAN}={180}^o$

Suy ra $\widehat{PAN}={180}^o-{33}^o={147}^o$.

Mặt khác, $\widehat{NAQ}=\widehat{PAM}={33}^o$ (hai góc đối đỉnh)

$\widehat{MAQ}=\widehat{PAN}={147}^o$ (hai góc đối đỉnh).

Vậy số đo các góc còn lại là: $\widehat{PAN}={147}^o$; $\widehat{NAQ}={33}^o$; $\widehat{MAQ}={147}^o$.

b) Vẽ tia At là tia phân giác của $\widehat{PAN}$ (như hình vẽ):

Vì tia At là tia phân giác của $\widehat{PAN}$ nên:

$\widehat{tAP}=\widehat{tAN}=\frac{\widehat{PAN}}{2}$

$=\frac{{147}^o}{2}=73,5^o$.

Ta có:

$\widehat{tAQ}=\widehat{tAN}+\widehat{NAQ}$

$=73,5^o+{33}^o=106,5^o$.

Tia At’ là tia đối của tia At (như hình vẽ).

Tia At’ nằm giữa hai tia AM và AQ (1)

Ta có: $\widehat{tAP}=\widehat{t\text{'}AQ}$ (hai góc đối đỉnh);

$\widehat{tAN}=\widehat{t\text{'}AM}$ (hai góc đối đỉnh).

Mà $\widehat{tAP}=\widehat{t\text{'}AN}$ (vì tia At là tia phân giác của $\widehat{PAN}$).

Suy ra $\widehat{t\text{'}AQ}=\widehat{t\text{'}AM}$ (2)

Từ (1) và (2) suy ra: At’ là tia phân giác của $\widehat{MAQ}$.

Bài 4 trang 75 Toán 7 Tập 1: Cho đường thẳng xy đi qua điểm O. Vẽ tia Oz sao cho $\widehat{xOz}={135}^o$. Vẽ tia Ot sao cho $\widehat{yOt}={90}^o$ và $\widehat{zOt}={135}^o.$ Gọi Ov là tia phân giác của $\widehat{xOt}$. Các góc $\widehat{xOv}$ và $\widehat{yOz}$ có phải là hai góc đối đỉnh không? Vì sao?

Lời giải:

Vì $\widehat{yOt}={90}^o$ mà $\widehat{xOy}$ là góc bẹt nên $\widehat{xOt}={90}^o$.

Tia Ov là tia phân giác của $\widehat{xOt}$ nên:

$\widehat{xOv}=\widehat{tOv}$ và $\widehat{xOv}+\widehat{tOv}={90}^o$.

Suy ra $\widehat{xOv}=\frac{\widehat{xOt}}{2}=\frac{{90}^o}{2}={45}^o$.

Tia Ox nằm giữa hai tia Oz và Ov nên:

$\widehat{vOz}=\widehat{xOv}+\widehat{xOz}$

Suy ra $\widehat{vOz}={45}^o+{135}^o={180}^o$.

Khi đó, tia Oz và Ov là hai tia đối nhau.

Mặt khác, đường thẳng xy đi qua điểm O nên Ox và Oy là hai tia đối nhau.

Do đó, tia Ox của $\widehat{xOv}$ là tia đối của tia Oy của $\widehat{yOz}$

Và tia Ov của $\widehat{xOv}$ là tia đối của tia Oz của $\widehat{yOz}$.

Vậy $\widehat{xOv}$ và $\widehat{yOz}$ là hai góc đối đỉnh.

Bài 5 trang 75 Toán 7 Tập 1: Vẽ hai góc kề bù $\widehat{xOy}$, $\widehat{yOx\text{'}}$, biết $\widehat{xOy}={142}^o$. Gọi Oz là tia phân giác của $\widehat{xOy}$. Tính $\widehat{x\text{'}Oz}$.

Lời giải:

Vì $\widehat{xOy}$, $\widehat{yOx\text{'}}$ là hai góc kề bù nên:

$\widehat{xOy}+\widehat{yOx\text{'}}={180}^o$

${142}^o+\widehat{yOx\text{'}}={180}^o$

Suy ra $\widehat{yOx\text{'}}={180}^o-{142}^o={38}^o$.

Tia Oz là tia phân giác của $\widehat{xOy}$ nên:

$\widehat{xOz}=\widehat{yOz}$ và $\widehat{xOz}+\widehat{yOz}={142}^o$.

Suy ra $\widehat{yOz}=\frac{\widehat{xOy}}{2}=\frac{{142}^o}{2}={71}^o$.

Tia Oy nằm giữa hai tia Ox’ và Oz nên:

$\widehat{x\text{'}Oz}=\widehat{x\text{'}Oy}+\widehat{yOz}$

Do đó $\widehat{x\text{'}Oz}={71}^o+{38}^o={109}^o$.

Vậy $\widehat{x\text{'}Oz}={109}^o$.

Bài 6 trang 75 Toán 7 Tập 1: Vẽ hai góc kề bù $\widehat{xOy},\widehat{yOx\text{'}}$, biết $\widehat{xOy}={120}^o$. Gọi Oz là tia phân giác của $\widehat{xOy}$, Oz’ là tia phân giác của $\widehat{yOx\text{'}}$. Tính $\widehat{zOy},\widehat{yOz\text{'}},\widehat{zOz\text{'}}$.

Lời giải:

$\widehat{xOy}$ và $\widehat{yOx\text{'}}$ là hai góc kề bù nên:

$\widehat{xOy}+\widehat{yOx\text{'}}={180}^o$

${120}^o+\widehat{yOx\text{'}}={180}^o$

Suy ra $\widehat{yOx\text{'}}={180}^o-{120}^o={60}^o$.

Tia Oz là tia phân giác của $\widehat{xOy}$ nên:

$\widehat{xOz}=\widehat{zOy}$ và $\widehat{xOz}+\widehat{zOy}={120}^o$.

Suy ra $\widehat{zOy}=\frac{\widehat{xOy}}{2}=\frac{{120}^o}{2}={60}^o$.

Tia Oz’ là tia phân giác của $\widehat{yOx\text{'}}$ nên:

$\widehat{yOz\text{'}}=\widehat{x\text{'}Oz\text{'}}$ và $\widehat{yOz\text{'}}+\widehat{x\text{'}Oz\text{'}}={60}^o$.

Suy ra $\widehat{yOz\text{'}}=\frac{\widehat{yOx\text{'}}}{2}=\frac{{60}^o}{2}={30}^o$.

Ta có:

 $\widehat{zOz\text{'}}=\widehat{zOy}+\widehat{yOz\text{'}}={60}^o+{30}^o={90}^o$

Vậy $\widehat{zOy}={60}^o,\widehat{yOz\text{'}}={30}^o,\widehat{zOz\text{'}}={90}^o$.

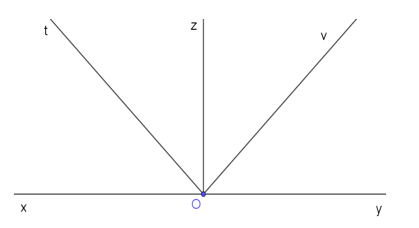
Bài 7 trang 75 Toán 7 Tập 1: Vẽ góc bẹt $\widehat{xOy}$. Vẽ tia phân giác Oz của góc đó. Vẽ tia phân giác Ot của $\widehat{xOz}$. Vẽ tia phân giác Ov của $\widehat{zOy}$. Tính $\widehat{tOv}$.

Lời giải:

Tia Oz là tia phân giác của $\widehat{xOy}$ nên:

$\widehat{xOz}=\widehat{zOy}$ và $\widehat{xOz}+\widehat{zOy}={180}^o$.

Suy ra $\widehat{zOy}=\frac{\widehat{xOy}}{2}=\frac{{180}^o}{2}={90}^o$.

Tia Ot là tia phân giác của $\widehat{xOz}$ nên:

$\widehat{xOt}=\widehat{zOt}$ và $\widehat{xOt}+\widehat{zOt}={90}^o$.

Suy ra $\widehat{zOt}=\frac{\widehat{xOz}}{2}=\frac{{90}^o}{2}={45}^o$.

Tia Ov là tia phân giác của $\widehat{yOz}$ nên:

$\widehat{zOv}=\widehat{yOv}$ và $\widehat{zOv}+\widehat{yOv}={90}^o$.

Suy ra $\widehat{zOv}=\frac{\widehat{yOv}}{2}=\frac{{90}^o}{2}={45}^o$.

Tia Oz nằm giữa hai tia Ot và Ov nên:

$\widehat{tOv}=\widehat{tOz}+\widehat{zOv}$

Do đó $\widehat{tOv}={45}^o+{45}^o={90}^o$.

Vậy $\widehat{tOv}={90}^o$.

Lời giải bài tập Toán lớp 7 Bài 2: Tia phân giác Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 73 Tập 1
• Giải Toán 7 trang 74 Tập 1