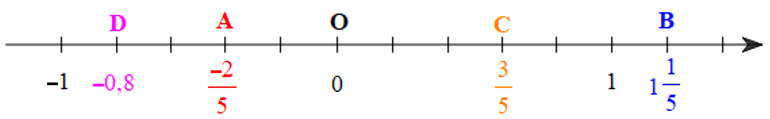Giải Toán 7 trang 9 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 9 Tập 1 trong Bài 1: Tập hợp các số hữu tỉ Toán lớp 7 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 9.

Giải Toán 7 trang 9 Tập 1 Chân trời sáng tạo

Thực hành 4 trang 9 Toán 7 Tập 1: Tìm số đối của của mỗi số sau: 7; $\frac{-5}{9}$; –0,75; 0; $1\frac{2}{3}$.

Lời giải:

Ta có: 

–7 là số đối của 7.

$\frac{5}{9}$ là số đối của $\frac{-5}{9}$.

0,75 là số đối của –0,75.

0 là số đối của 0.

-$1\frac{2}{3}$ là số đối của $1\frac{2}{3}$.

Vận dụng 2 trang 9 Toán 7 Tập 1: Bạn Hồng đã phát biểu: “4,1 lớn hơn 3,5. Vì thế –4,1 cũng lớn hơn –3,5”.

Theo em, phát biểu của bạn Hồng có đúng không? Tại sao?

Lời giải:

Ta có –4,1 = $\frac{-41}{10}$ và –3,5 = $\frac{-35}{10}$.

Mà –41 < –35 nên $\frac{-41}{10}$ < $\frac{-35}{10}$.

Do đó –4,1 < –3,5.

Vậy phát biểu của bạn Hồng không đúng.

Bài 1 trang 9 Toán 7 Tập 1: Thay 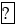bằng kí kiệu ∈, ∉ thích hợp.

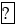
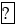
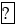
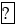
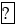
-7 ℕ;                  -17 ℤ;;                -38 ℚ;

$\frac{4}{5}$ ℤ;                  $\frac{4}{5}$ ℚ;               0,25 ℤ;               3,25 ℚ

Lời giải:

Ta có – 7 là một số nguyên âm nên –7 không thuộc ℕ, ta viết: -7 $\boxed{\notin }$ ℕ;

Ta có –17 là một số nguyên âm nên –17 thuộc ℤ, ta viết: -17 $\boxed{\in }$ ℤ;

Ta có -38 = $\frac{-38}{1}$, trong đó 1 ∈ ℤ và 1 ≠ 0 nên -38 $\boxed{\in }$ ℚ

Ta có 4; 5 ∈ ℤ và 5 ≠ 0 nên $\frac{4}{5}$ là một số hữu tỉ và không là một số nguyên, do đó ta viết $\frac{4}{5}\boxed{\notin }\mathbb{Z}$ và $\frac{4}{5}\boxed{\in }\mathbb{Q}$;

Ta có 0,25 không là một số nguyên nên 0,25 $\boxed{\notin }$ ℤ;

Ta có 3,25 = $\frac{325}{100}=\frac{13}{4}$, trong đó 13; 4 ∈ ℤ và 4 ≠ 0, do đó 3,25 $\boxed{\in }$ ℚ.

Bài 2 trang 9 Toán 7 Tập 1:

a) Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ $\frac{-5}{9}$ ?

$\frac{-10}{18};\frac{10}{18};\frac{15}{-27};-\frac{20}{36};\frac{-25}{27}$.

b) Tìm số đối của mỗi số sau: 12; $\frac{4}{9}$; -0,375; $\frac{0}{5}$; -$2\frac{2}{5}$.

Lời giải:

a) Ta có

$\frac{-10}{18}=\frac{\left(-10\right):2}{18:2}=\frac{-5}{9}$;              $\frac{10}{18}=\frac{10:2}{9:2}=\frac{5}{9}$;

$\frac{15}{-27}=\frac{15:\left(-3\right)}{\left(-27\right):\left(-3\right)}=\frac{-5}{9}$;              $-\frac{20}{36}=-\frac{20:4}{36:4}=-\frac{5}{9}=\frac{-5}{9}$.

Vậy những phân số biểu diễn số hữu tỉ $\frac{-5}{9}$ là: $\frac{-10}{18};\frac{15}{-27};-\frac{20}{36}$.

b) Ta có: 

Số đối của 12 là số –12.

Số đối của $\frac{4}{9}$ là số $\frac{-4}{9}$.

Số đối của –0,375 là số 0,375.

Số đối của $\frac{0}{5}$ = 0 là số 0.

Số đối của $2\frac{2}{5}$ là số $-2\frac{2}{5}$.

Bài 3 trang 9 Toán 7 Tập 1:

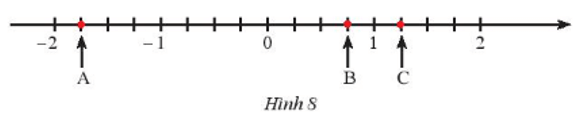
a) Các điểm A; B; C trong Hình 8 biểu diễn số hữu tỉ nào?

b) Biểu diễn các số hữu tỉ $\frac{-2}{5};1\frac{1}{5};\frac{3}{5};-0,8$ trên trục số.

Lời giải:

a) Ta thấy từ điểm 0 đến điểm 1 và từ điểm –1 đến điểm 0 đều chia thành 4 đoạn bằng nhau, nên đoạn đơn vị mới bằng $\frac{1}{4}$ đoạn đơn vị cũ.

Điểm A nằm bên trái điểm 0 một đoạn bằng 7 đơn vị mới nên điểm A biểu diễn điểm $\frac{-7}{4}$.

Điểm B nằm bên phải điểm 0 một đoạn bằng 3 đơn vị mới nên điểm B biểu diễn điểm $\frac{3}{4}$.

Điểm C nằm bên phải điểm 0 một đoạn bằng 5 đơn vị mới nên điểm C biểu diễn điểm $\frac{5}{4}$.

b) Ta có $1\frac{1}{5}=\frac{1.5+1}{5}=\frac{6}{5}$ và -0,8 = $\frac{-8}{10}=\frac{-4}{5}$

Chia đoạn thẳng đơn vị thành 5 phần bằng nhau, ta được đoạn đơn vị mới bằng $\frac{1}{5}$ đơn vị cũ.

Như vậy các điểm $\frac{-2}{5};\frac{6}{5};\frac{3}{5};\frac{-4}{5}$ lần lượt:

• được biểu biễn bởi điểm A nằm về bên trái điểm 0 cách 0 một đoạn bằng 2 phần đơn vị mới;

• được biểu biễn bởi điểm B nằm về bên phải điểm 0 cách 0 một đoạn bằng 6 phần đơn vị mới;

• được biểu biễn bởi điểm C nằm về bên phải điểm 0 cách 0 một đoạn bằng 3 phần đơn vị mới;

• được biểu biễn bởi điểm D nằm về bên trái điểm 0 cách 0 một đoạn bằng 4 phần đơn vị mới.

Lời giải bài tập Toán lớp 7 Bài 1: Tập hợp các số hữu tỉ Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 6 Tập 1
• Giải Toán 7 trang 7 Tập 1
• Giải Toán 7 trang 8 Tập 1
• Giải Toán 7 trang 10 Tập 1