Giải Toán 7 trang 78 Tập 2 Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 78 Tập 2 trong Bài 8: Tính chất ba đường cao của tam giác Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 78.
Giải Toán 7 trang 78 Tập 2 Chân trời sáng tạo
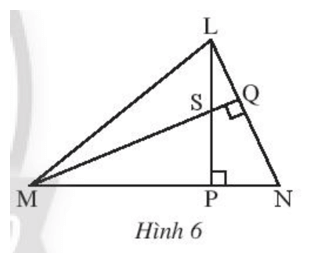
Thực hành 2 trang 78 Toán 7 Tập 2: Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6).
Chứng minh rằng NS vuông góc với ML.
Lời giải:
Tam giác LMN có hai đường cao LP và MQ cắt nhau tại S nên S là trực tâm của tam giác LMN.
Do đó NS vuông góc với ML.
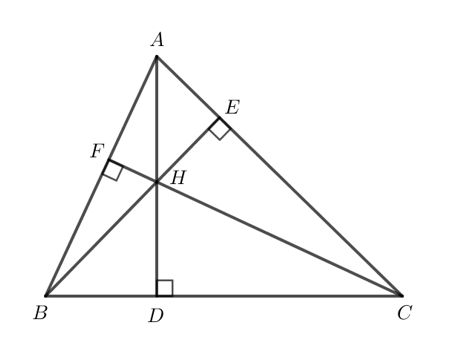
Vận dụng 2 trang 78 Toán 7 Tập 2: Cho tam giác ABC có ba đường cao AD, BE, CF đồng quy tại trực tâm H. Tìm trực tâm của các tam giác HBC, HAB, HAC.
Lời giải:
Tam giác HBC có HD BC, BF HC nên HD và BF là hai đường cao của tam giác HBC.
Mà HD và BF cắt nhau tại A nên A là trực tâm của tam giác HBC.
Tam giác HAB có HF AB, BD AH nên HF, BD là hai đường cao của tam giác HAB.
Mà HF và BD cắt nhau tại C nên C là trực tâm của tam giác HAB.
Tam giác HAC có HE AC, CD AH nên HE, CD là hai đường cao của tam giác HAC.
Mà HE và CD cắt nhau tại B nên B là trực tâm của tam giác HAC.
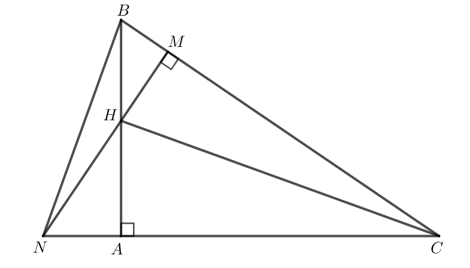
Bài 1 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Lấy điểm H thuộc cạnh AB. Vẽ HM vuông góc với BC tại M. Tia MH cắt tia CA tại N. Chứng minh rằng CH vuông góc với NB.
Lời giải:
Tam giác BNC có BA NC, NM BC nên BA, NM là hai đường cao của tam giác BNC.
Mà BA và NM cắt nhau tại H nên H là trực tâm của tam giác BNC.
Do đó CH vuông góc với NB.
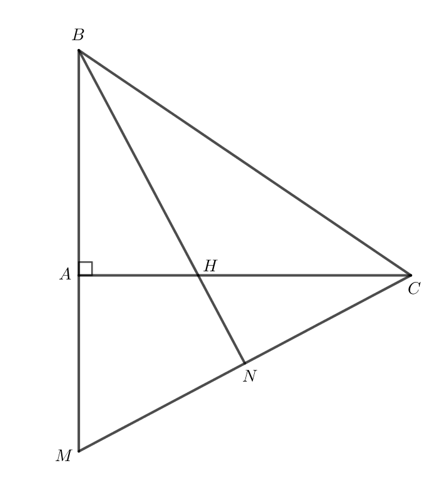
Bài 2 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông tại A. Trên tia BA lấy điểm M sao cho BM = BC. Tia phân giác của góc B cắt AC tại H. Chứng minh rằng MH vuông góc với BC.
Lời giải:
Tam giác BMC có BM = BC nên tam giác BMC cân tại B.
Tam giác BMC cân tại B, có BN là đường phân giác nên BN cũng là đường cao của tam giác BMC.
Do đó BN MC.
Tam giác BMC có CA BM, BN MC nên CA, BN là hai đường cao của tam giác BMC.
Mà CA và BN cắt nhau tại H nên H là trực tâm của tam giác BMC.
Do đó MH BC.
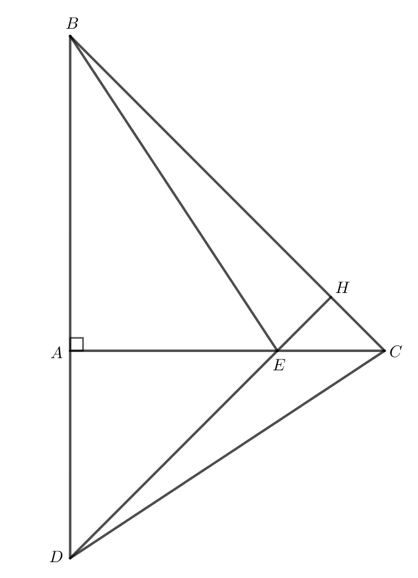
Bài 3 trang 78 Toán 7 Tập 2: Cho tam giác ABC vuông cân tại A. Lấy điểm E thuộc cạnh AC. Trên tia đối của tia AB lấy điểm D sao cho AD = AE. Chứng minh rằng:
a) DE vuông góc với BC;
b) BE vuông góc với DC.
Lời giải:
Gọi giao điểm của DE và BC là H.
Tam giác ABC vuông cân tại A nên (trong tam giác vuông, tổng hai góc nhọn bằng ) và .
Do đó .
Tam giác vuông ADE có AD = AE nên tam giác ADE vuông cân tại A.
Khi đó và .
Do đó .
Ta có là góc ngoài tại đỉnh E của tam giác EDC nên .
Do đó .
Khi đó trong tam giác DHC:
.
.
.
Do đó DH BC.
b) Tam giác BDC có CA BD, DH BC nên CA, DH là hai đường cao của tam giác BDC.
Mà CA và DH cắt nhau tại E nên E là trực tâm của tam giác BDC.
Do đó BE vuông góc với DC.
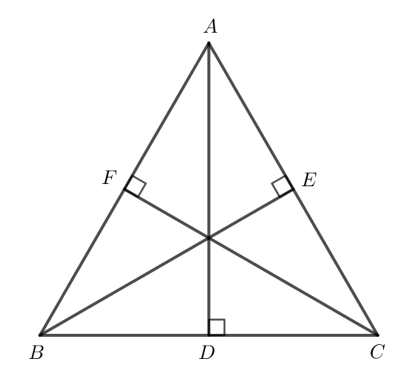
Bài 4 trang 78 Toán 7 Tập 2: Cho tam giác nhọn ABC có ba đường cao AD, BE, CF. Biết AD = BE = CF. Chứng minh rằng tam giác ABC đều.
Lời giải:
Xét vuông tại F và vuông tại E có:
CF = BE (theo giả thiết).
BC chung.
Do đó (cạnh huyền - cạnh góc vuông).
Suy ra (2 góc tương ứng).
Tam giác ABC có nên tam giác ABC cân tại A.
Do đó AB = AC (1).
Xét vuông tại E và vuông tại D có:
BE = AD (theo giả thiết).
AB chung.
Do đó (cạnh huyền - cạnh góc vuông).
Suy ra (2 góc tương ứng).
Tam giác ABC có nên tam giác ABC cân tại C.
Do đó CA = CB (2).
Từ (1) và (2) ta có AB = BC = CA nên tam giác ABC đều.
Lời giải bài tập Toán lớp 7 Bài 8: Tính chất ba đường cao của tam giác Chân trời sáng tạo hay khác: