b) Chứng minh rằng với mọi điểm M thì AM < AB.
Câu hỏi:
b) Chứng minh rằng với mọi điểm M thì AM < AB.
Trả lời:
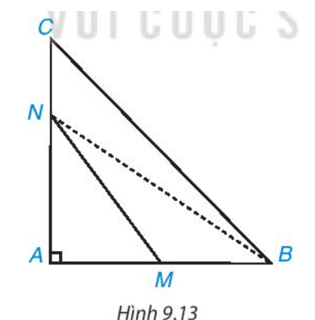
b) Ta xét các trường hợp sau:
• M nằm giữa B và H: là góc tù nên DABM là tam giác tù.
Khi đó cạnh AB đối diện với là cạnh lớn nhất của DABM.
Hay AM < AB (1)
• M trùng với H: AH, AB lần lượt là đường vuông góc, đường xiên kẻ từ A đến BC.
Khi đó AH là đường ngắn nhất nên AH = AM < AB (2)
• M nằm giữa H và C: là góc tù nên DAMC là tam giác tù.
Khi đó cạnh AC đối diện với là cạnh lớn nhất của DAMC.
Hay AM < AC
Mà AB = AC (do DABC cân tại A).
Do đó AM < AB (3)
Từ (1), (2) và (3) ta có AM < AB.
Vậy AM < AB.