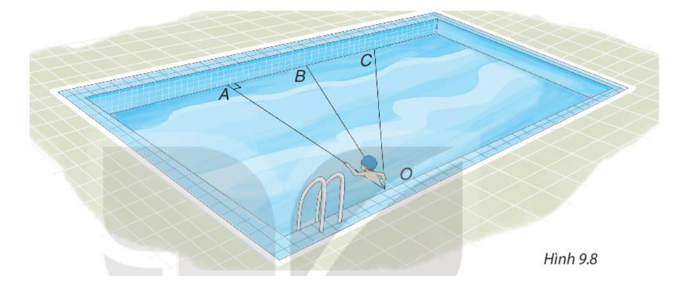
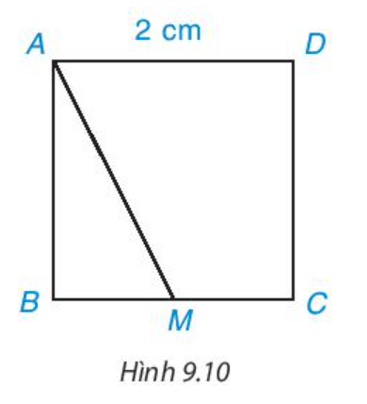
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị
Câu hỏi:
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Trả lời:
b)
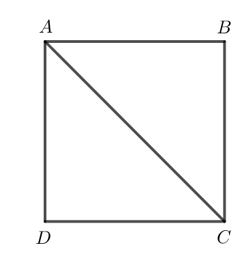
Nếu M nằm trên AB hoặc AD thì AM ≤ AB (AM = AB khi điểm M trùng điểm B).
Nếu M nằm trên BC hoặc CD thì AM ≤ AC (AM = AD khi điểm M trùng điểm B).
Mà AB = AD (do ABCD là hình vuông)
Do đó nếu M nằm trên cạnh AB hoặc AD thì AM ≤ AB (1)
• Nếu M nằm trên cạnh BC thì BM ≤ BC
Theo khẳng định của câu a) ta có AM ≤ AC (AM = AC khi điểm M trùng điểm C).
Tương tự, nếu M nằm trên cạnh DC thì AM ≤ AC.
Do đó nếu M nằm trên cạnh BC hoặc DC thì AM ≤ AC (2)
• Ta có AB là đường vuông góc kẻ từ A đến BC, AC là đường xiên kẻ từ A đến BC nên AB là đường ngắn nhất
Do đó AC ≥ AB (3).
Từ (1), (2) và (3) suy ra AM ≤ AB ≤ AC.
Suy ra AM lớn nhất bằng AC.
Khi đó M trùng C.
Vậy M trùng C thì AM lớn nhất.