Câu hỏi:
b) Đỉnh nào cách đều hai đường thẳng AB và AD?
Trả lời:
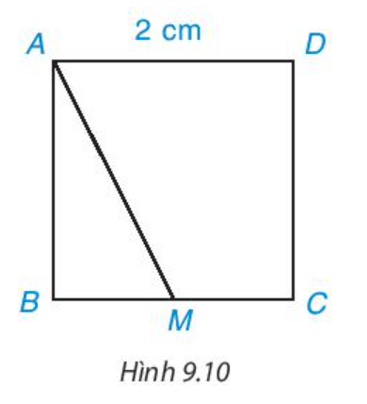
b) CB là khoảng cách từ C đến AB, CD là khoảng cách từ C đến AD.
BC = CD nên khoảng cách từ C đến AB bằng khoảng cách từ C đến AD.
Do đó C là điểm cách đều hai đường thẳng AB và AD.
Mặt khác, AB ⊥ AD tại A nên điểm A cũng cách đều hai đường thẳng AB và AD.
Vậy hai đỉnh C, A cách đều hai đường thẳng AB và AD.
Câu 1:
Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB và OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8).
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?
Câu 2:
Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.
Câu 4:
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
Câu 5:
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
Câu 7:
Cho tam giác ABC vuông tại A. Hai điểm M, N theo thứ tự nằm trên các cạnh AB, AC (M, N không phải là đỉnh của tam giác) (H.9.13). Chứng minh rằng MN < BC.
(Gợi ý. So sánh MN với NB, NB với BC).
