Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD
Câu hỏi:
Ba bạn Mai, Việt và Hà đi đến trường tại địa điểm D lần lượt theo ba con đường AD, BD và CD (H.9.7). Biết rằng ba điểm A, B, C cùng nằm trên một đường thẳng, B nằm giữa A và C, là góc tù. Hỏi bạn nào đi xa nhất, bạn nào đi gần nhất? Vì sao?
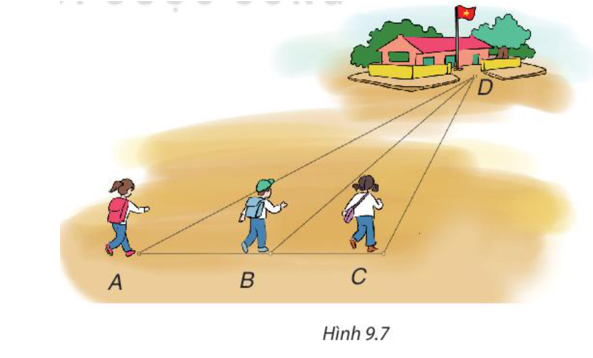
Trả lời:
Ta có là góc ngoài tại đỉnh B của nên .
Do đó là góc tù.
Xét có là góc tù nên DABD là tam giác tù
Suy ra cạnh AD đối diện với là cạnh lớn nhất trong .
Khi đó AD > BD (1).
Xét DBCD có là góc tù nên DBCD là tam giác tù
Suy ra cạnh BD đối diện với là cạnh lớn nhất của DBCD.
Cạnh đối diện với trong là cạnh BD.
Do đó cạnh BD là cạnh lớn nhất trong .
Khi đó BD > CD (2).
Từ (1) và (2) suy ra AD > BD > CD.
Vậy bạn Mai đi xa nhất, bạn Hà đi gần nhất