Bài 4.30 trang 86 Toán 7 Tập 1 - Kết nối tri thức
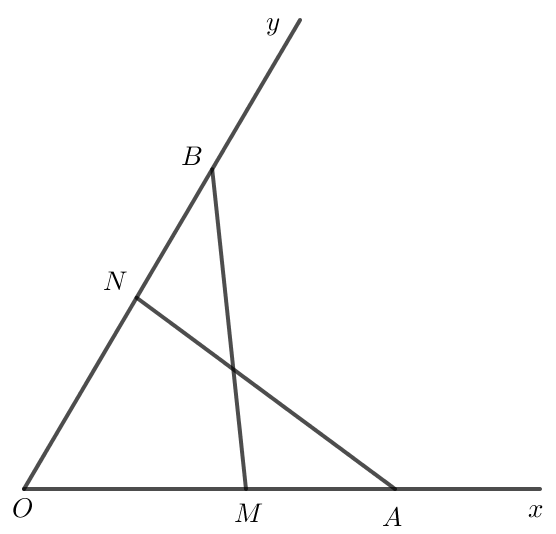
Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:
Giải Toán lớp 7 Luyện tập chung trang 85, 86
Bài 4.30 trang 86 Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho OA = OB, OM = ON, OA > OM. Chứng minh rằng:
a)
b)
Lời giải:
a)
Xét hai tam giác OAN và OBM có:
OA = OB (theo giả thiết).
chung.
ON = OM (theo giả thiết).
Vậy (c – g – c).
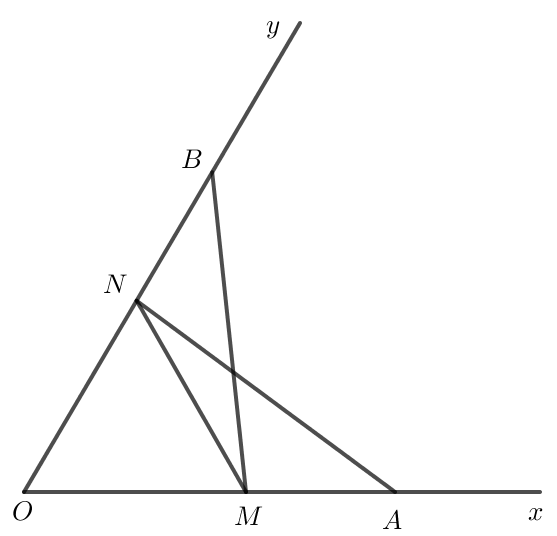
b)
Do nên AN = BM (2 cạnh tương ứng).
Có BN = OB – ON, AM = OA – OM.
Mà OB = OA, ON = OM nên BN = AM.
Xét hai tam giác AMN và BNM có:
AM = BN (chứng minh trên).
MN chung.
AN = BM (chứng minh trên).
Vậy (c – c – c).
Lời giải bài tập Toán lớp 7 Luyện tập chung trang 86 Kết nối tri thức hay khác: