Bài 4.31 trang 86 Toán 7 Tập 1 - Kết nối tri thức

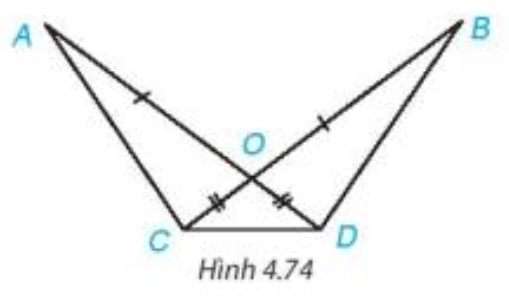
Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:

Giải Toán lớp 7 Luyện tập chung trang 85, 86

Bài 4.31 trang 86 Toán 7 Tập 1: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng:

a) AC = BD;

b) $\Delta AC\text{D}=\Delta B\text{D}C.$

Lời giải:

a) Xét hai tam giác AOC và BOD có:

OA = OB (theo giả thiết).

$\widehat{AOC}=\widehat{BO\text{D}}$ (2 góc đối đỉnh).

OC = OD (theo giả thiết).

Do đó $\Delta AOC=\Delta BO\text{D}$ (c – g – c).

Vậy AC = BD (2 cạnh tương ứng).

b) Có AD = OA + OD, BC = OB + OC.

Mà OA = OB, OC = OD nên AD = BC.

Xét hai tam giác ACD và BDC có:

AD = BC (chứng minh trên).

AC = BD (chứng minh trên).

CD chung.

Vậy $\Delta AC\text{D}=\Delta B\text{D}C$ (c – c – c).

Lời giải bài tập Toán lớp 7 Luyện tập chung trang 86 Kết nối tri thức hay khác:

• Bài 4.29 trang 86 Toán 7 Tập 1: Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ. ....

• Bài 4.30 trang 86 Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho ....

• Bài 4.32 trang 86 Toán 7 Tập 1: Cho tam giác MBC vuông tại M có $\widehat{B}=60°.$ Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều. ....