Bài 4.32 trang 86 Toán 7 Tập 1 - Kết nối tri thức

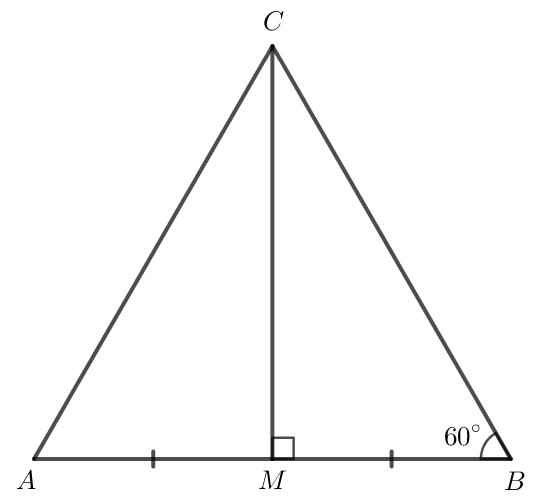
Cho tam giác MBC vuông tại M có  Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Giải Toán lớp 7 Luyện tập chung trang 85, 86

Bài 4.32 trang 86 Toán 7 Tập 1: Cho tam giác MBC vuông tại M có $\widehat{B}=60°.$ Gọi A là điểm nằm trên tia đối của tia MB sao cho MA = MB. Chứng minh rằng tam giác ABC là tam giác đều.

Lời giải:

Xét hai tam giác AMC vuông tại M và BMC vuông tại M có:

AM = BM (theo giả thiết).

MC chung.

Do đó $\Delta AMC=\Delta BMC$ (2 cạnh góc vuông).

Khi đó AC = BC (2 cạnh tương ứng).

Tam giác ABC có AC = BC nên tam giác ABC cân tại C.

Tam giác ABC cân tại C lại có $\widehat{ABC}=60°$ nên tam giác ABC là tam giác đều.

Vậy tam giác ABC là tam giác đều.

Lời giải bài tập Toán lớp 7 Luyện tập chung trang 86 Kết nối tri thức hay khác:

• Bài 4.29 trang 86 Toán 7 Tập 1: Cho Hình 4.73. Hãy tính các độ dài a, b và số đo x, y của các góc trên hình vẽ. ....

• Bài 4.30 trang 86 Toán 7 Tập 1: Cho góc xOy. Trên tia Ox lấy hai điểm A, M; trên tia Oy lấy hai điểm B, N sao cho ....

• Bài 4.31 trang 86 Toán 7 Tập 1: Cho Hình 4.74, biết OA = OB, OC = OD. Chứng minh rằng: ....