Bài 9.28 trang 81 Toán 7 Tập 2 - Kết nối tri thức
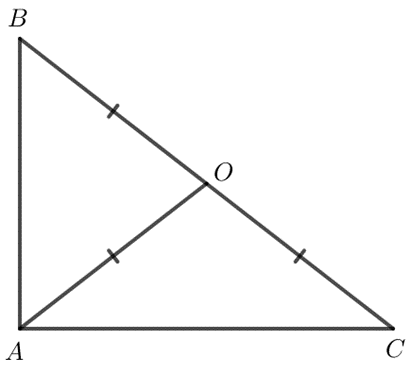
Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Giải Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
Bài 9.28 trang 81 Toán 7 Tập 2: Xét điểm O cách đều ba đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông.
Lời giải:
Giả sử O nằm trên cạnh BC.
Do OA = OB nên ∆OAB cân tại O.
Do đó .
Do OA = OC nên ∆OAC cân tại O.
Do đó .
Khi đó hay .
Xét ∆ABC có .
Mà nên hay .
Do đó ∆ABC vuông tại A.
Vậy nếu O nằm trên một cạnh của tam giác ABC và O cách đều ba đỉnh của tam giác ABC thì ABC là một tam giác vuông.
Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác:
Câu hỏi trang 77 Toán 7 Tập 2: Mỗi tam giác có mấy đường trung trực? ....
Vận dụng 1 trang 79 Toán 7 Tập 2: Em hãy trả lời câu hỏi trong tình huống mở đầu ....
Câu hỏi trang 79 Toán 7 Tập 2: Mỗi tam giác có mấy đường cao? ....