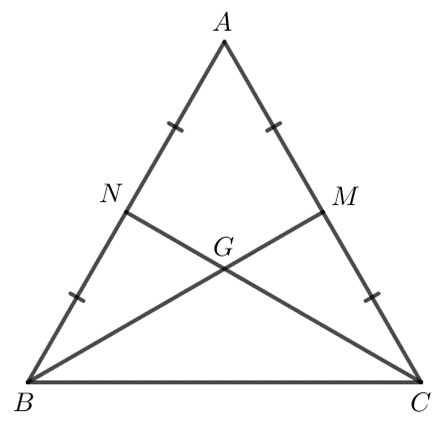
Luyện tập 1 trang 79 Toán 7 Tập 2 - Kết nối tri thức

Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.

Giải Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác

Luyện tập 1 trang 79 Toán 7 Tập 2: Chứng minh rằng trong tam giác đều ABC, trọng tâm G cách đều ba đỉnh của tam giác đó.

Lời giải:

Luyện tập 1 trang 79 Toán 7 Tập 2 | Kết nối tri thức Giải Toán lớp 7

Gọi M là giao điểm của BG và AC, N là giao điểm của CG và AB.

Do ∆ABC đều nên AB = BC = CA và $\hat{A B C} = \hat{A C B} = \hat{B A C}$ .

M là trung điểm của AC nên AM = MC.

Xét ∆ABM và ∆CBM có:

AB = CB (chứng minh trên).

$\hat{B A M} = \hat{B C M}$ (chứng minh trên).

AM = CM (chứng minh trên).

Suy ra ∆ABM = ∆CBM (c - g - c).

Do đó $\hat{B M A} = \hat{B M C}$ (2 góc tương ứng).

Mà $\hat{B M A} + \hat{B M C} = 180 °$ nên $\hat{B M A} = \hat{B M C} = 90 °$ .

Do đó BM ⊥ AC.

BM vuông góc với AC tại trung điểm M của AC nên BM là đường trung trực của AC.

N là trung điểm của AB nên AN = BN.

Xét ∆CAN và ∆CBN có:

CA = CB (chứng minh trên).

$\hat{C A N} = \hat{C B N}$ (chứng minh trên).

AN = BN (chứng minh trên).

Suy ra ∆CAN = ∆CBN (c - g - c).

Do đó $\hat{C N A} = \hat{C N B}$ (2 góc tương ứng).

Mà $\hat{C N A} + \hat{C N B} = 180 °$ nên $\hat{C N A} = \hat{C N B} = 90 °$ .

Do đó CN ⊥ AB.

CN vuông góc với AB tại trung điểm N của AB nên CN là đường trung trực của AB.

G là giao điểm 2 đường trung trực của ∆ABC nên G cách đều 3 đỉnh của tam giác.

Lời giải bài tập Toán 7 Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác hay, chi tiết khác: