Bài 9.38 trang 84 Toán 7 Tập 2 - Kết nối tri thức
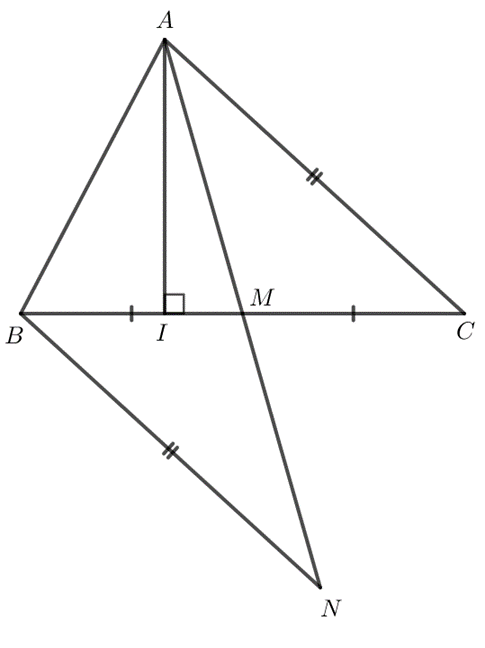
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
Giải Toán 7 Bài tập cuối chương 9
Bài 9.38 trang 84 Toán 7 Tập 2: Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng:
a) AI < (AB + AC);
b) AM < (AB + AC).
Lời giải:
a) ∆AIB vuông tại I nên AB là cạnh huyền.
Do đó AB > AI (1).
∆AIC vuông tại I nên AC là cạnh huyền.
Do đó AC > AI (2).
Từ (1) và (2) ta có 2AI < AB + AC hay AI < (AB + AC).
b) Từ B kẻ BN song song với AC sao cho BN = AC.
Do BN // AC nên (2 góc so le trong).
Do AM là đường trung tuyến của ∆ABC nên M là trung điểm của BC.
M là trung điểm của BC nên BM = CM.
Xét ∆NBM và ∆ACM có:
BM = CM (chứng minh trên).
(chứng minh trên).
BN = CA (giả thiết).
Suy ra ∆NBM = ∆ACM (c - g - c).
Suy ra AM = MN (2 cạnh tương ứng) và (2 góc tương ứng).
Do nên hay .
Suy ra A, M, N thẳng hàng.
Lại có AM = MN nên M là trung điểm của AN suy ra AN = 2AM.
Xét ∆ABN có AB + BN > AN hay AB + BN > 2AM.
Mà BN = AC nên AB + AC > 2AM.
Do đó AM < (AB + AC).
Lời giải bài tập Toán 7 Bài tập cuối chương 9 hay, chi tiết khác: