Bài 9.8 trang 65 Toán 7 Tập 2 - Kết nối tri thức
Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
Giải Toán 7 Bài 32: Quan hệ đường vuông góc và đường xiên
Bài 9.8 trang 65 Toán 7 Tập 2: Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C (H.9.12).
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì AM < AB.
Lời giải:
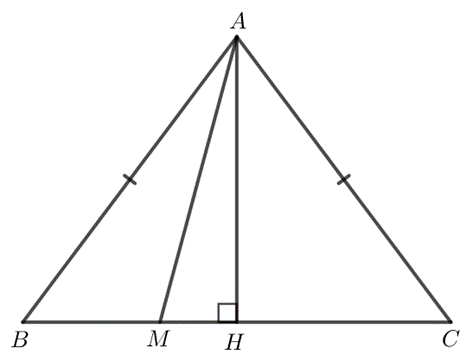
a)
Kẻ AH vuông góc với BC tại H.
M di chuyển trên BC thì AM ≥ AH.
Do đó giá trị nhỏ nhất của AM là AH.
AM = AH khi M trùng H.
Vậy M là chân đường cao kẻ từ A đến BC thì giá trị của AM nhỏ nhất.
b) là góc ngoài tại đỉnh M của ∆AMC nên
Do ∆ABC cân tại A nên .
Do đó .
Xét ∆AMB có nên AB > AM.
Vậy AM < AB.
Lời giải bài tập Toán 7 Bài 32: Quan hệ giữa đường vuông góc và đường xiên hay, chi tiết khác: