Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD = 2DC.
Câu hỏi:
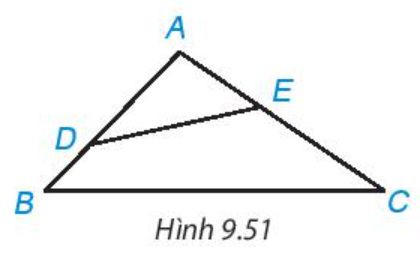
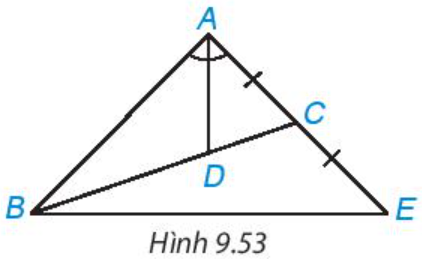
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD = 2DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A.
Gợi ý. D là trọng tâm của tam giác ABE, tam giác này có đường phân giác AD đồng thời là đường trung tuyến.
Trả lời:
Xét tam giác ABE có: C là trung điểm của AE nên BC là đường trung tuyến của tam giác ABE.
Ta lại có D là điểm nằm trên BC sao cho BD = 2DC.
Ta có: BC = BD + DC = 2DC + DC = 3DC.
Do đó, BC = 3DC và BC = 2BD hay .
Điểm D thuộc trung tuyến BC thỏa mãn nên D là trọng tâm tam giác ABE.
Suy ra AD là đường trung tuyến của tam giác ABE.
Xét tam giác ABE có:
AD vừa là đường trung tuyến, vừa là đường phân giác nên theo Ví dụ 1 phần Luyện tập chung, trang 82, DABE cân tại A.