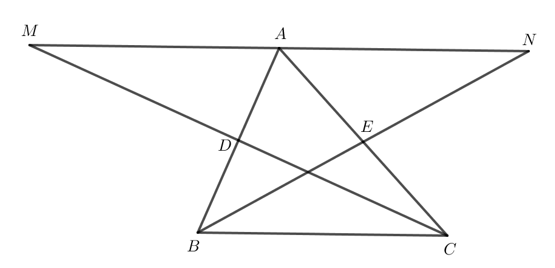
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC,

Câu hỏi:

Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho DM = DC.

a) Chứng minh rằng $Δ A D M = Δ B D C$ . Từ đó suy ra AM = BC và AM // BC.

Trả lời:

a) Vì D là trung điểm của AB nên AD = BD.

Xét $Δ A D M$ và $Δ B D C$ có:

$\hat{A D M} = \hat{B D C}$ (2 góc đối đỉnh).

DM = DC (theo giả thiết).

AD = BD (chứng minh trên).

Suy ra $Δ A D M = Δ B D C$ (c - g - c).

Do đó AM = BC (2 cạnh tương ứng) và $\hat{M A D} = \hat{C B D}$ (2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên AM // BC.

Câu 1:

Tính giá trị của các biểu thức sau:

a) $\sqrt{25}$ + (2² . 3)² . ${(- \frac{1}{4})}^{2}$ + 2020⁰ + $|- \frac{1}{4}|$ ;

Câu 2:

\frac{3^{2} - 0, 25. (7, 5 - 5, 1)}{- 6, 2 + 2. (0, 5 + 1, 6)}

Xem lời giải »

Câu 3:

Tính một cách hợp lí.

a) $\frac{5}{11} - \frac{10}{19} + 1, 5 + \frac{17}{11} - \frac{9}{19}$ ;

Câu 4:

b) $2 \frac{3}{5} . (- \frac{2}{3}) - 2 \frac{1}{3} . (- \frac{2}{3}) + {(\frac{2}{3})}^{2}$

Câu 5:

b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho EN = EB. Chứng minh rằng AN // BC.

Câu 6:

c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.

Câu 7:

Cho tam giác cân ABC tại đỉnh A. Gọi H là trung điểm của BC.

a) Chứng minh AH $⊥$ BC.

Câu 8:

b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho BM = CN. Chứng minh rằng $Δ A B M = Δ A C N$ .

Giải Toán lớp 7 Kết nối tri thức