Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng
Câu hỏi:
Chứng minh rằng tam giác có đường trung tuyến và đường cao xuất phát từ cùng một đỉnh trùng nhau là một tam giác cân.
Trả lời:
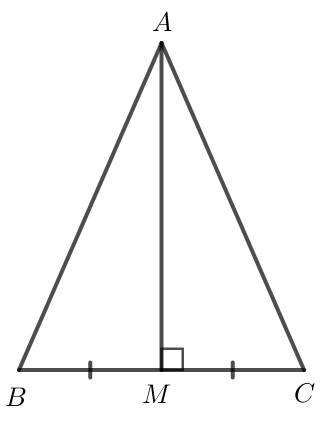
Giả sử tam giác ABC có AM vừa là đường trung tuyến, vừa là đường cao xuất phát từ đỉnh A.
Do AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.
Do đó BM = CM.
Xét vuông tại M và vuông tại M có:
AM chung.
BM = CM (chứng minh trên).
Suy ra (2 cạnh góc vuông).
Do đó AB = AC (2 cạnh tương ứng).
Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

