Giải Toán 7 trang 71 Tập 1 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 71 Tập 1 trong Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Toán lớp 7 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 71.

Giải Toán 7 trang 71 Tập 1 Kết nối tri thức

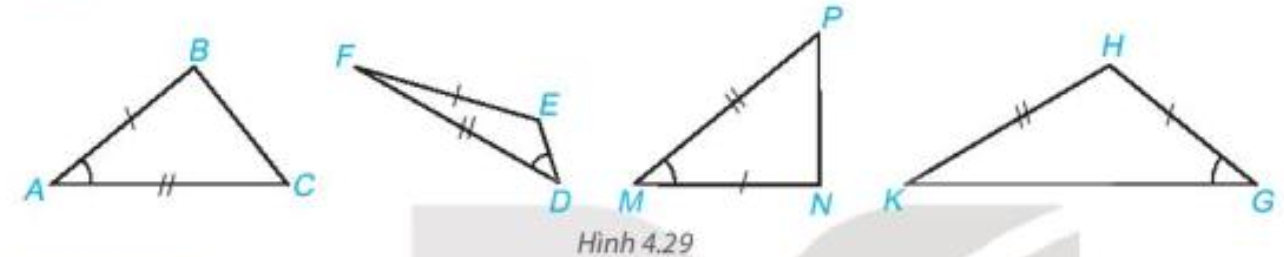
Câu hỏi trang 71 Toán 7 Tập 1: Trong Hình 4.29, hai tam giác nào bằng nhau?

Lời giải:

Hai tam giác DEF và GHK có góc D không phải góc xen giữa hai cạnh EF, FD và góc G không phải góc xen giữa hai cạnh GH, HK nên ta không thực hiện xét hai tam giác này.

Xét hai tam giác ABC và MNP có:

AB = MN (theo giả thiết).

$\widehat{BAC}=\widehat{NMP}$ (theo giả thiết).

AC = MP (theo giả thiết).

Do đó $\Delta ABC=\Delta MNP$ (c – g – c).

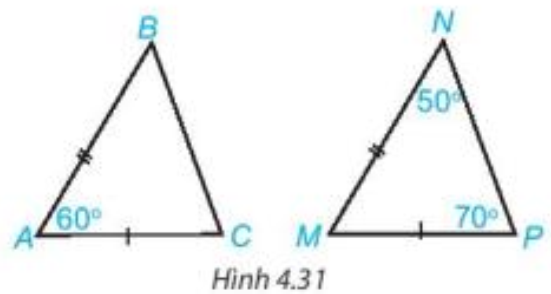
Luyện tập 1 trang 71 Toán 7 Tập 1: Hai tam giác ABC và MNP trong Hình 4.31 có bằng nhau không? Vì sao?

Lời giải:

Xét tam giác MNP có $\widehat{M}+\widehat{N}+\widehat{P}=180°.$

Do đó $\widehat{M}=180°-\widehat{N}-\widehat{P}=180°-50°-70°=60°.$

Xét hai tam giác ABC và MNP có:

AB = MN (theo giả thiết).

$\widehat{BAC}=\widehat{NMP}$ (cùng bằng 60^o).

AC = MP (theo giả thiết).

Vậy $\Delta ABC=\Delta MNP$ (c – g – c).

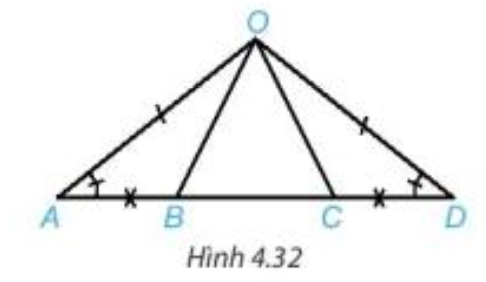
Vận dụng trang 71 Toán 7 Tập 1: Cho Hình 4.32, biết $\widehat{OAB}=\widehat{O\text{D}C},$ OA = OD và AB = CD. Chứng minh rằng:

a) AC = DB;

b) $\Delta OAC=\Delta O\text{DB.}$

Lời giải:

a) Do AB = CD nên AB + BC = CD + BC.

hay AC = DB.

Vậy AC = DB.

b) Xét hai tam giác OAC và ODB có:

OA = OD (theo giả thiết).

$\widehat{OAC}=\widehat{O\text{D}B}$ (theo giả thiết).

AC = BD (chứng minh trên).

Vậy $\Delta OAC=\Delta O\text{D}B$ (c – g – c).

Lời giải bài tập Toán lớp 7 Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Kết nối tri thức hay khác:

• Giải Toán 7 trang 70 Tập 1
• Giải Toán 7 trang 72 Tập 1
• Giải Toán 7 trang 73 Tập 1