Giải Toán 7 trang 64 Tập 2 Kết nối tri thức
Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 64 Tập 2 trong Bài 32: Quan hệ đường vuông góc và đường xiên Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 64.
Giải Toán 7 trang 64 Tập 2 Kết nối tri thức
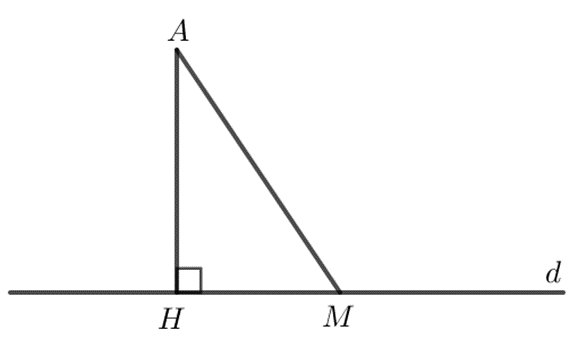
HĐ trang 64 Toán 7 Tập 2: Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.
b) Em hãy giải thích vì sao AH < AM.
Lời giải:
a)
b) Do AH ⊥ d nên = 90o.
Xét ∆AHM có = 90o nên là góc lớn nhất trong ∆AHM.
Do đó AM là cạnh lớn nhất trong ∆AHM.
Do đó AH < AM.
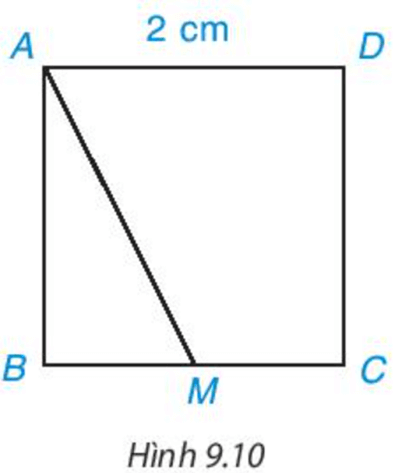
Luyện tập trang 64 Toán 7 Tập 2: Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
b) So sánh hai đoạn thẳng AB và AM.
c) Tìm khoảng cách từ điểm C đến đường thẳng AB.
Lời giải:
a) Đường vuông góc kẻ từ A đến đường thẳng BC là AB.
Đường xiên kẻ từ A đến đường thẳng BC là AM.
b) Do AM là đường xiên kẻ từ A đến BC và AB là đường vuông góc kẻ từ A đến BC nên AM > AB.
c) Khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn BC.
Do ABCD là hình vuông nên BC = AD = 2 cm.
Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.
Vận dụng trang 64 Toán 7 Tập 2: Em hãy trả lời câu hỏi trong tình huống mở đầu.
Lời giải:
Ta có OA là đường vuông góc kẻ từ O đến AC.
OB và OC là các đường xiên kẻ từ O đến AC nên OB > OA và OC > OA.
Do đó để bơi sang bờ bên kia nhanh nhất thì Nam nên chọn đường bơi OA.
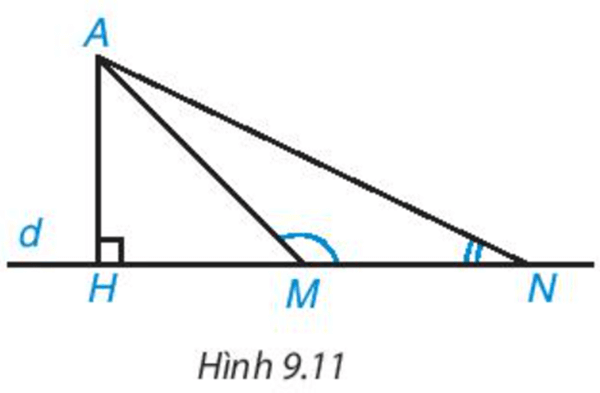
Thử thách nhỏ trang 64 Toán 7 Tập 2: a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.
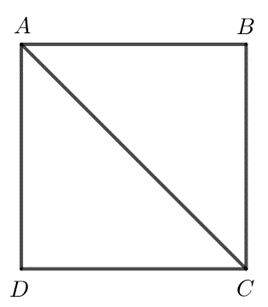
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Lời giải:
a) Với HM < HN ta có là góc ngoài tại đỉnh M của ∆AHM do đó .
Do đó là góc tù.
∆AMN có là góc tù nên là góc lớn nhất trong ∆AMN.
Do đó AN là cạnh lớn nhất trong ∆AMN hay AM < AN.
b)
Nếu M nằm trên AB hoặc AD thì AM ≤ AB (1).
Nếu M nằm trên BC hoặc CD thì AM ≤ AC (2).
Ta có AB là đường vuông góc kẻ từ A đến BC, AC là đường xiên kẻ từ A đến BC nên AC > AB.
Do đó từ (1) và (2) suy ra AM lớn nhất bằng AC.
Khi đó M trùng C.
Vậy M trùng C thì AM lớn nhất.
Lời giải bài tập Toán lớp 7 Bài 32: Quan hệ đường vuông góc và đường xiên Kết nối tri thức hay khác: