Bài 4 trang 97 Toán 8 Tập 1 Cánh diều

Cho một tam giác đều cạnh a.

Giải Toán 8 Bài 1: Định lí Pythagore - Cánh diều

Bài 4 trang 97 Toán 8 Tập 1: Cho một tam giác đều cạnh a.

a) Tính độ dài đường cao của tam giác đó theo a.

b) Tính diện tích của tam giác đó theo a.

Lời giải:

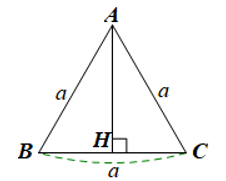
Giả sử ABC là tam giác đều cạnh a (hình vẽ).

Bài 4 trang 97 Toán 8 Tập 1 Cánh diều | Giải Toán 8

a) Vẽ đường cao AH của tam giác đều ABC.

Khi đó H là trung điểm của BC nên HB = HC = $\frac{1}{2} a$ .

Xét tam giác AHC vuông tại H, theo định lí Pythagore ta có:

AC² = AH² + HC²

Suy ra AH² = AC² – HC²

$= a^{2} - {(\frac{1}{2} a)}^{2} = a^{2} - \frac{1}{4} a^{2} = \frac{3}{4} a^{2} = {(\frac{\sqrt{3}}{2})}^{2} . a^{2} = {(\frac{a \sqrt{3}}{2})}^{2}$

Do đó $A H = \frac{a \sqrt{3}}{2}$ .

b) Diện tích của tam giác ABC là:

$S = \frac{1}{2} . A H . B C = \frac{1}{2} . \frac{a \sqrt{3}}{2} . a = \frac{a^{2} \sqrt{3}}{4}$ (đơn vị diện tích).

Lời giải bài tập Toán 8 Bài 1: Định lí Pythagore hay, chi tiết khác: