Khởi động trang 94 Toán 8 Tập 1 Cánh diều
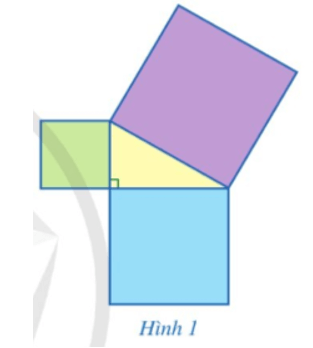
Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Giải Toán 8 Bài 1: Định lí Pythagore - Cánh diều
Khởi động trang 94 Toán 8 Tập 1: Quan sát Hình 1, bạn Đan khẳng định rằng: Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Bạn Đan đã dựa vào kiến thức nào để đưa ra khẳng định trên?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Bạn Đan đã dựa vào Định lí Pythagore để đưa ra khẳng định “Diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại”.
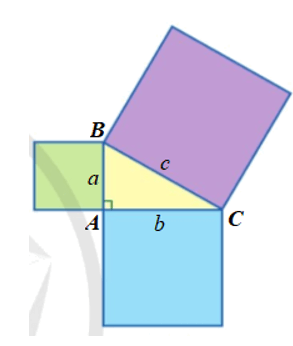
Thật vậy, giả sử A, B, C là ba đỉnh của tam giác (vuông tại A) và độ dài cạnh của các hình vuông lần lượt là a, b, c (hình vẽ).
Diện tích hình vuông nhỏ màu xanh lá cây là: a2 (đơn vị diện tích).
Diện tích hình vuông nhỏ màu xanh nước biển là: b2 (đơn vị diện tích).
Diện tích hình vuông lớn màu tím là: c2 (đơn vị diện tích).
Do tam giác ABC vuông tại A nên theo định lí Pythagore ta có BC2 = AB2 + AC2
Hay c2 = a2 + b2.
Vậy diện tích của hình vuông lớn nhất bằng tổng diện tích của hai hình vuông còn lại.
Lời giải bài tập Toán 8 Bài 1: Định lí Pythagore hay, chi tiết khác: