Giải Toán 8 trang 69 Tập 2 Cánh diều

---

Với Giải Toán 8 trang 69 Tập 2 trong Bài 4: Tính chất đường phân giác của tam giác Toán 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 69.

Giải Toán 8 trang 69 Tập 2 Cánh diều

Bài 1 trang 69 Toán 8 Tập 2: Cho tam giác ABC có ba đường phân giác AD, BE, CF. Biết AB = 4, BC = 5, CA = 6. Tính BD, CE, AF.

Lời giải:

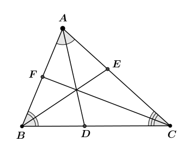
Áp dụng tính chất đường phân giác cho tam giác ABC, ta có:

⦁ $\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ (do AD là đường phân giác của góc BAC)

Suy ra $\frac{\mathrm{DB}}{\mathrm{BC}-\mathrm{DB}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ hay $\frac{\mathrm{BD}}{5-\mathrm{BD}}=\frac{4}{6}$

Do đó 6BD = 4(5 – BD)

          6BD = 20 – 4BD

          6BD + 4BD = 20

          10BD = 20

          BD = 2.

⦁$\frac{\mathrm{EC}}{\mathrm{EA}}=\frac{\mathrm{BC}}{\mathrm{BA}}$ (do BE là đường phân giác của góc ABC)

Suy ra $\frac{\mathrm{EC}}{\mathrm{AC}-\mathrm{EC}}=\frac{\mathrm{BC}}{\mathrm{BA}}$ hay $\frac{\mathrm{CE}}{6-\mathrm{CE}}=\frac{5}{4}$

Do đó 4CE = 5(6 – CE)

          4CE = 30 – 5CE

          4CE + 5CE = 30

          9CE = 30

          $\mathrm{CE}=\frac{30}{9}=\frac{10}{3}$

⦁$\frac{\mathrm{FA}}{\mathrm{FB}}=\frac{\mathrm{CA}}{\mathrm{CB}}$ (do CF là đường phân giác của góc ACB)

Suy ra $\frac{\mathrm{FA}}{\mathrm{AB}-\mathrm{FA}}=\frac{\mathrm{CA}}{\mathrm{CB}}$ hay $\frac{\mathrm{AF}}{4-\mathrm{AF}}=\frac{6}{5}$

Do đó 5AF = 6(4 – AF)

          5AF = 24 – 6AF

          5AF + 6AF = 24

          11AF = 24

         $\mathrm{AF}=\frac{24}{11}.$

Bài 2 trang 69 Toán 8 Tập 2: Cho tam giác ABC có đường trung tuyến AM. Tia phân giác của góc ABC lần lượt cắt các đoạn thẳng AM, AC tại điểm D, E. Chứng minh $\frac{EC}{EA}=2\frac{DM}{DA}.$

Lời giải:

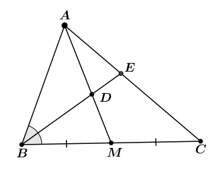
Theo tính chất đường phân giác trong tam giác, ta có:

⦁ $\frac{\mathrm{EC}}{\mathrm{EA}}=\frac{\mathrm{BC}}{\mathrm{BA}}$ (do BE là đường phân giác của góc ABC trong ∆ABC);

⦁ $\frac{\mathrm{DM}}{\mathrm{DA}}=\frac{\mathrm{BM}}{\mathrm{BA}}$ (do BD là đường phân giác của góc ABM trong ∆ABM).

Mà BC = 2BM (do AM là đường trung tuyến của ∆ABC)

Suy ra $\frac{\mathrm{EC}}{\mathrm{EA}}=\frac{\mathrm{BC}}{\mathrm{BA}}=2\frac{\mathrm{BM}}{\mathrm{BA}}=2\frac{\mathrm{DM}}{\mathrm{DA}}.$

Vậy $\frac{\mathrm{EC}}{\mathrm{EA}}=2\frac{\mathrm{DM}}{\mathrm{DA}}.$

Bài 3 trang 69 Toán 8 Tập 2: Quan sát Hình 43 và chứng minh $\frac{\mathrm{DB}}{\mathrm{DC}}:\frac{\mathrm{EB}}{\mathrm{EG}}=\frac{\mathrm{AG}}{\mathrm{AC}}.$

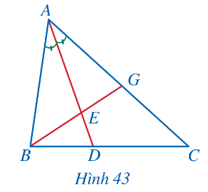
Lời giải:

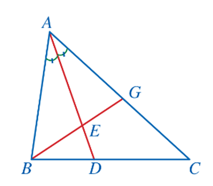
⦁ $\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ (do AD là đường phân giác của góc BAC trong ∆ABC);

⦁ $\frac{\mathrm{EB}}{\mathrm{EG}}=\frac{\mathrm{AB}}{\mathrm{AG}}$ (do AE là đường phân giác của góc BAG trong ∆ABG).

Suy ra: $\frac{\mathrm{DB}}{\mathrm{DC}}:\frac{\mathrm{EB}}{\mathrm{EG}}=\frac{\mathrm{AB}}{\mathrm{AC}}:\frac{\mathrm{AB}}{\mathrm{AG}}=\frac{\mathrm{AB}}{\mathrm{AC}}\cdot \frac{\mathrm{AG}}{\mathrm{AB}}=\frac{\mathrm{AG}}{\mathrm{AC}}$

Vậy $\frac{\mathrm{DB}}{\mathrm{DC}}:\frac{\mathrm{EB}}{\mathrm{EG}}=\frac{\mathrm{AG}}{\mathrm{AC}}.$

Theo tính chất đường phân giác trong tam giác, ta có:

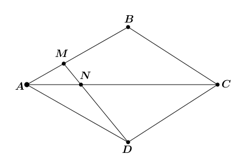
Bài 4 trang 69 Toán 8 Tập 2: Cho hình thoi ABCD (Hình 44). Điểm M thuộc cạnh AB thoả mãn AB = 3AM. Hai đoạn thẳng AC và DM cắt nhau tại N. Chứng minh ND = 3MN.

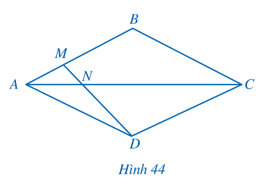
Lời giải:

Do ABCD là hình thoi nên AD = AB và AC là đường phân giác của góc BAC.

Xét ∆AMD có AN là đường phân giác góc MAD nên $\frac{\mathrm{ND}}{\mathrm{NM}}=\frac{\mathrm{AD}}{\mathrm{AM}}$

Hay $\frac{\mathrm{ND}}{\mathrm{NM}}=\frac{\mathrm{AD}}{\frac{1}{3}\mathrm{AB}}$ (vì AB = 3AM)

Do đó $\frac{\mathrm{ND}}{\mathrm{NM}}=\frac{\mathrm{AB}}{\frac{1}{3}\mathrm{AB}}=3$

Vậy ND = 3MN.

Bài 5 trang 69 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có AB = 3, AC = 4, AD là đường phân giác. Tính:

a) Độ dài các đoạn thẳng BC, DB, DC;

b) Khoảng cách từ điểm D đến đường thẳng AC;

c) Độ dài đường phân giác AD.

Lời giải:

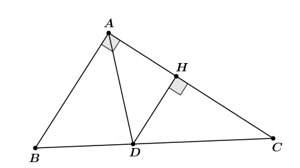
a) Xét tam giác ABC vuông tại A, theo định lí Pythagore, ta có:

BC² = AB² + AC² = 3² + 4² = 25 = 5²

Suy ra BC = 5.

Theo tính chất đường phân giác trong tam giác, ta có: $\frac{\mathrm{DB}}{\mathrm{DC}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ (do AD là đường phân giác của góc BAC)

Suy ra $\frac{\mathrm{DB}}{\mathrm{BC}-\mathrm{DB}}=\frac{\mathrm{AB}}{\mathrm{AC}}$ hay $\frac{\mathrm{DB}}{5-\mathrm{DB}}=\frac{3}{4}$

Do đó 4DB = 3(5 – DB)

          4DB = 15 – 3DB

          4DB + 3DB = 15

          7DB = 15

          $\mathrm{DB}=\frac{15}{7}$

Khi đó $\mathrm{DC}=\mathrm{BC}-\mathrm{DB}=5-\frac{15}{7}=\frac{20}{7}$

Vậy $\mathrm{BC}=5;\mathrm{DB}=\frac{15}{7};\mathrm{DC}=\frac{20}{7}.$

b) Kẻ DH ⊥ AC (H ∈ AC).

Suy ra DH // AB (cùng vuông góc với AC)

Áp dụng hệ quả của định lí Thalès trong tam giác ABC với DH // AB, ta có:

$\frac{\mathrm{DH}}{\mathrm{BA}}=\frac{\mathrm{CD}}{\mathrm{CB}}$ hay $\frac{\mathrm{DH}}{3}=\frac{\frac{20}{7}}{5}$

Suy ra $\mathrm{DH}=\frac{3\cdot \frac{20}{7}}{5}=\frac{12}{7}$

Vậy khoảng cách từ điểm D đến đường thẳng AC là $\mathrm{DH}=\frac{12}{7}.$

c) Xét tam giác ABC với DH // AB, ta có: $\frac{\mathrm{AH}}{\mathrm{AC}}=\frac{\mathrm{BD}}{\mathrm{BC}}$ (hệ quả của định lí Thalès)

Hay $\frac{\mathrm{AH}}{4}=\frac{\frac{15}{7}}{5},$ suy ra $\mathrm{AH}=\frac{4\cdot \frac{15}{7}}{5}=\frac{12}{7}$

Xét tam giác AHD vuông tại H, ta có: AD² = AH² + DH² (định lí Pythagore)

Suy ra ${\mathrm{AD}}^2={\left(\frac{12}{7}\right)}^2+{\left(\frac{12}{7}\right)}^2=\frac{288}{49}$

Do đó $\mathrm{AD}=\sqrt{\frac{288}{49}}=\sqrt{\frac{144\cdot 2}{49}}=\sqrt{{\left(\frac{12\sqrt{2}}{7}\right)}^2}=\frac{12\sqrt{2}}{7}$

Vậy độ dài đường phân giác AD là $\frac{12\sqrt{2}}{7}.$

Bài 6 trang 69 Toán 8 Tập 2: Cho tứ giác ABCD với các tia phân giác của các góc CAD và CBD cùng đi qua điểm E thuộc cạnh CD (Hình 45 . Chứng minh AD.BC = AC.BD.

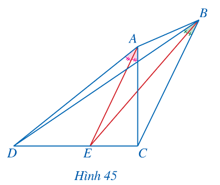
Lời giải:

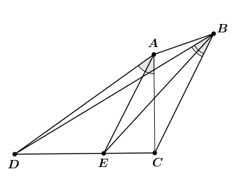
Theo tính chất đường phân giác trong hai tam giác ACD và BCD, ta có:

⦁ $\frac{\mathrm{EC}}{\mathrm{ED}}=\frac{\mathrm{AC}}{\mathrm{AD}}$ (do AE là đường phân giác của góc CAD);

⦁ $\frac{\mathrm{EC}}{\mathrm{ED}}=\frac{\mathrm{BC}}{\mathrm{BD}}$ (do BE là đường phân giác của góc CBD).

Suy ra $\frac{\mathrm{AC}}{\mathrm{AD}}=\frac{\mathrm{BC}}{\mathrm{BD}}$

Vậy AD.BC = AC.BD.

Lời giải bài tập Toán 8 Bài 4: Tính chất đường phân giác của tam giác hay khác:

• Giải Toán 8 trang 66

• Giải Toán 8 trang 67

• Giải Toán 8 trang 68