Giải Toán 8 trang 82 Tập 2 Cánh diều
Với Giải Toán 8 trang 82 Tập 2 trong Bài 7: Trường hợp đồng dạng thứ hai của tam giác Toán 8 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 82.
Giải Toán 8 trang 82 Tập 2 Cánh diều
Bài 2 trang 82 Toán 8 Tập 2: Cho Hình 75, chứng minh:
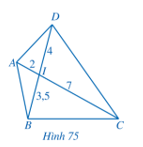
a) ∆IAB ᔕ ∆IDC;
b) ∆IAD ᔕ ∆IBC.
Lời giải:
a) Ta có Suy ra
Xét ∆IAB và ∆IDC có:
(đối đỉnh) và
Vậy ∆IAB ᔕ ∆IDC (c.g.c).
b) Ta có Suy ra
Xét ∆IAD và ∆IBC có:
(đối đỉnh) và
Vậy ∆IAD ᔕ ∆IBC (c.g.c).
Bài 3 trang 82 Toán 8 Tập 2: Cho Hình 76, biết AB = 4, BC = 3, BE = 2, BD = 6. Chứng minh:
a) ∆ABD ᔕ ∆EBC;
b)
c) Tam giác DGE vuông.
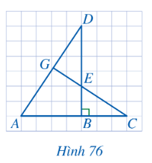
Lời giải:
a) Ta có Suy ra
Xét∆ABD và ∆EBCcó:
và
Vậy ∆ABD ᔕ ∆EBC (c.g.c).
b) Do ∆ABD ᔕ ∆EBC (câu a), suy ra (hai góc tương ứng)
Mà (đối đỉnh) nên
c) Ta có (tổng hai góc nhọn của ∆ABD vuông tại B bằng 90°)
Mà (câu b)
Suy ra hay
Xét ∆GDE có (tổng ba góc của một tam giác)
Suy ra
Vậy tam giác DGE vuông tại G.
Bài 4 trang 82 Toán 8 Tập 2: Cho Hình 77, chứng minh:
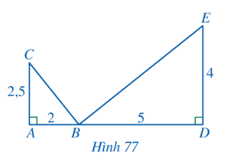
a)
b) BC ⊥ BE.
Lời giải:
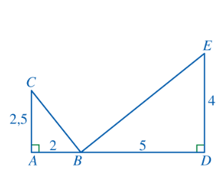
a) Ta có Suy ra
Xét ∆ABC và ∆DEB có:
Suy ra ∆ABC ᔕ ∆DEB (c.g.c).
Do đó (hai góc tương ứng).
b) Ta có (tổng hai góc nhọn của ∆BDE vuông tại D bằng 90°)
Mà (câu a)
Suy ra
Lại có
Nên
Do đó BC ⊥ BE.
Bài 5 trang 82 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆MNP.
a) Gọi D và Q lần lượt là trung điểm của BC và NP. Chứng minh ∆ABD ᔕ ∆MNQ.
b) Gọi G và K lần lượt là trọng tâm của hai tam giác ABC và MNP. Chứng minh ∆ABG ᔕ ∆MNK.
Lời giải:
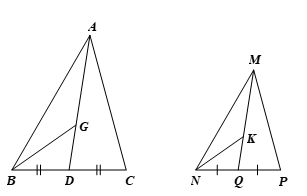
a) Vì ∆ABC ᔕ ∆MNP (giả thiết) nên và
Vì D, Q lần lượt là trung điểm của BC và NP nên
Do đó suy ra
Xét ∆ABDvà ∆MNQ có:
(do
Suy ra ∆ABD ᔕ ∆MNQ (c.g.c).
b) Vì ∆ABD ᔕ ∆MNQ (câu a) (hai góc tương ứng) và (tỉ số đồng dạng)
Mà G, K lần lượt là trọng tâm của hai tam giác ABC và MNP nên
Do đó
Xét ∆ABG và ∆MNK có:
(do
Vậy ∆ABG ᔕ ∆MNK (c.g.c).
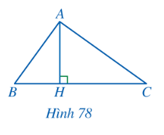
Bài 6 trang 82 Toán 8 Tập 2: Cho Hình 78, biết AH2 = BH.CH. Chứng minh:
a) ∆HAB ᔕ ∆HCA;
b) Tam giác ∆ABC vuông tại A.
Lời giải:
a) Từ AH2 = BH.CH ta có
Xét ∆HAB và ∆HCA có:
Suy ra ∆HAB ᔕ ∆HCA (c.g.c).
b) Vì ∆HAB ᔕ ∆HCA (câu a) nên (hai góc tương ứng).
Mà (tổng hai góc nhọn của ∆ABH vuông tại H bằng 90°)
Suy ra hay
Vậy ∆ABC vuông tại A.
Bài 7 trang 82 Toán 8 Tập 2: Đố. Chỉ sử dụng thước thẳng có chia đơn vị đến milimét và thước đo góc, làm thế nào đo được khoảng cách giữa hai vị trí B, C trên thực tế, biết rằng có vị trí A thoả mãn AB = 20 m, AC = 50 m,
Bạn Vy làm như sau: Vẽ tam giác A’B’C’ có A’B’ = 2 cm, A’C’ = 5 cm, Bạn Vy lấy thước đo khoảng cách giữa hai điểm B’, C’ và nhận được kết quả B’C’ ≈ 6,6 cm. Từ đó, bạn Vy kết luận khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66 m. Em hãy giải thích tại sao bạn Vy có thể kết luận như vậy.
Lời giải:
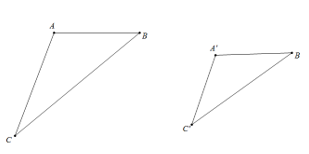
Đổi A’B’ = 2 cm = 0,02 m;
A’C’ = 5 cm = 0,05 m;
B’C’ = 6,6 cm = 0,066 m.
Ta có
Do đó
Xét ∆ABC và ∆A’B’C’ có:
Suy ra ∆ABC ᔕ ∆A’B’C’ (c.g.c)
Do đó
Nên BC = 1 000 . B’C’ = 1 000 . 0,066 = 66 (m).
Vậy khoảng cách giữa hai vị trí B, C trên thực tế khoảng 66m.
Lời giải bài tập Toán 8 Bài 7: Trường hợp đồng dạng thứ hai của tam giác hay khác:
