Khám phá 3 trang 83 Toán 8 Tập 1 Chân trời sáng tạo

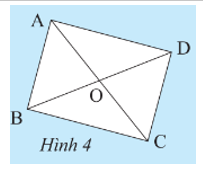
Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau:

Giải Toán 8 Bài 5: Hình chữ nhật – Hình vuông - Chân trời sáng tạo

Khám phá 3 trang 83 Toán 8 Tập 1: Cho hình bình hành ABCD có O là giao điểm của hai đường chéo. Giải thích các khẳng định sau:

a) Nếu $\hat{B A D}$ là góc vuông thì $\hat{A D C}$ và $\hat{A B C}$ cũng là góc vuông.

b) Nếu AC = BD thì $\hat{B A D}$ vuông.

Khám phá 3 trang 83 Toán 8 Tập 1 Chân trời sáng tạo | Giải Toán 8

Lời giải:

a) Do ABCD là hình bình hành nên AB // CD và AD // BC.

Do $\hat{B A D}$ là góc vuông nên AD ⊥ AB.

Ta có: AB // CD và AD ⊥ AB nên AD ⊥ CD hay $\hat{A D C}$ là góc vuông;

AD // BC và AD ⊥ AB nên BC ⊥ AB hay $\hat{A B C}$ là góc vuông.

b) Hình bình hành ABCD có AB // CD nên cũng là hình thang có hai cạnh đáy là AB và CD.

Lại có hai đường chéo AC = BD nên là hình thang cân.

Do đó $\hat{A B C} = \hat{D C B}$ và $\hat{B A D} = \hat{C D A}$ .

Tương tự ta cũng có $\hat{B A D} = \hat{A B C}$

Suy ra $\hat{B A D} = \hat{A B C} = \hat{D C B} = \hat{C D A}$

Mà $\hat{B A D} + \hat{A B C} + \hat{D C B} + \hat{C D A} = 360 °$

Hay $4 \hat{B A D} = 360 °$ , do đó $\hat{B A D} = 90 °$ .

Lời giải bài tập Toán 8 Bài 5: Hình chữ nhật – Hình vuông hay, chi tiết khác: