Giải Toán 8 trang 59 Tập 1 Chân trời sáng tạo

---

Với Giải Toán 8 trang 59 Tập 1 trong Bài 1: Định lí Pythagore Toán lớp 8 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 59.

Giải Toán 8 trang 59 Tập 1 Chân trời sáng tạo

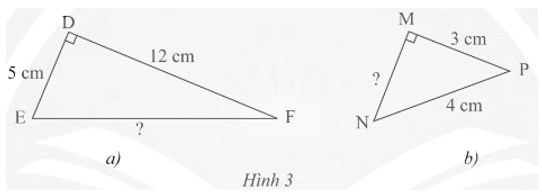
Thực hành 1 trang 59 Toán 8 Tập 1: Tính độ dài cạnh EF, MN của các tam giác vuông trong Hình 3.

Lời giải:

Hình 3a: Áp dụng định lí Pythagore vào tam giác vuông DEF có cạnh huyền EF, ta có:

EF² = DE² + DF²

Suy ra EF² = 5² + 12² = 25 + 144 = 169 = 13².

Vậy EF = 13 cm.

Hình 3b: Áp dụng định lí Pythagore vào tam giác vuông MNP có cạnh huyền NP, ta có:

NP² = MN² + MP²

Suy ra MN² = NP² – MP²

           MN² = 4² – 3² = 16 – 9 = 7.

Vậy EF = $\sqrt{7}$ cm.

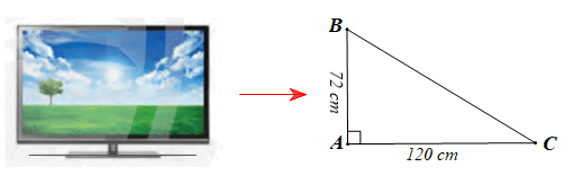
Vận dụng 1 trang 59 Toán 8 Tập 1: Một chiếc ti vi màn hình phẳng có chiều rộng và chiều dài đo được lần lượt là 72 cm và 120 cm. Tính độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch (biết 1 inch ≈ 2,54 cm).

Lời giải:

Chiếc ti vi ở Hình 4 được mô tả bởi tam giác ABC vuông tại A có các kích thước như hình vẽ sau:

Áp dụng định lí Pythagore vào tam giác ABC có cạnh huyền BC, ta có:

BC² = AB² + AC² = 72² + 120² = 5 184 + 14 400 = 19 584.

Suy ra BC = $24\sqrt{34}$ (cm).

Vậy độ dài đường chéo của màn hình chiếc ti vi đó theo đơn vị inch là:

$24\sqrt{34}:2,54\approx 55$ (inch).

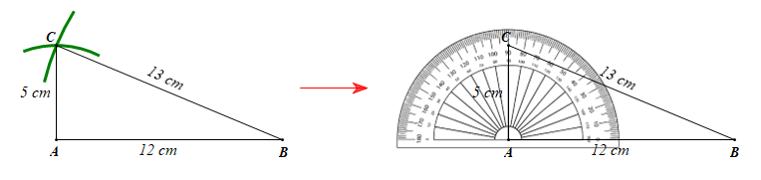
Khám phá 2 trang 59 Toán 8 Tập 1: Vẽ vào vở tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm, rồi xác định số đo $\widehat{BAC}$ bằng thước đo góc

Lời giải:

Ta vẽ tam giác ABC có AB = 12 cm, AC = 5 cm, BC = 13 cm như sau:

• Vẽ đoạn thẳng AB = 12 cm;

• Vẽ cung tròn tâm A bán kính 5 cm và cung tròn tâm B bán kính 13 cm. Hai cung tròn này cắt nhau tại một điểm, điểm này là điểm C.

Dùng thước đo góc (đặt thước như hình vẽ trên) ta xác định được $\widehat{BAC}=90°$.

Lời giải bài tập Toán 8 Bài 1: Định lí Pythagore Chân trời sáng tạo hay khác:

• Giải Toán 8 trang 58

• Giải Toán 8 trang 60

• Giải Toán 8 trang 61

• Giải Toán 8 trang 62