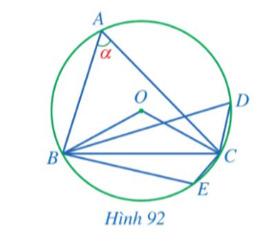
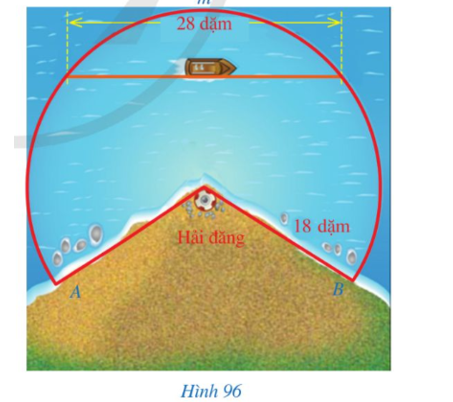
Câu hỏi:
Trả lời:
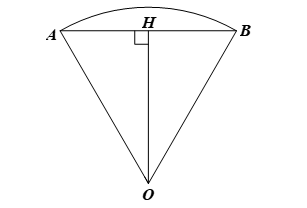
Kẻ OH ⊥ AB.
Xét ∆OAB có OA = OB = R và nên ∆OAB là tam giác đều. Do đó
Xét ∆OHA vuông tại H, ta có:
Diện tích phần logo màu xanh có dạng tam giác OAB là:
Diện tích phần logo màu đỏ có dạng hình viên phân là:
S2 = S – S1 ≈ 33,5 – 27,7 = 5,8 (cm2).
Câu 1:
Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O).
a) Số đo góc BOC là
Câu 5:
Hình 96 biểu diễn vùng biển được chiếu sáng bởi một hải đăng có dạng một hình quạt tròn với bán kính 18 dặm, cung AmB có số đo 245°.
a) Hãy tính diện tích vùng biển có thể nhìn thấy ánh sáng từ hải đăng theo đơn vị kilômét vuông (lấy 1 dặm = 1 609 m và làm tròn kết quả đến hàng đơn vị).
Câu 6:
b) Giả sử một con thuyền di chuyển dọc theo dây cung có độ dài 28 dặm của đường tròn với tâm là tâm của hình quạt tròn, bán kính là 18 dặm. Tính khoảng cách nhỏ nhất từ con thuyền đến hải đăng (theo đơn vị dặm và làm tròn kết quả đến hàng đơn vị).
