Bài 2 trang 51 Toán 9 Tập 2 Cánh diều

---

Cho hàm số

Giải Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) - Cánh diều

Bài 2 trang 51 Toán 9 Tập 2: Cho hàm số $y=\frac{1}{3}{x}^2.$

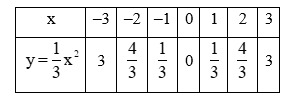
a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:

b) Dựa vào bảng giá trị trên, vẽ đồ thị của hàm số đó.

c) Tìm những điểm thuộc đồ thị của hàm số có hoành độ lần lượt bằng –6; 10.

d) Tìm những điểm thuộc đồ thị của hàm số có tung độ bằng 27.

Lời giải:

a) Xét hàm số $y=\frac{1}{3}{x}^2:$

⦁ Với x = –3 thì $y=\frac{1}{3}\cdot {\left(-3\right)}^2=3.$

⦁ Với x = –2 thì $y=\frac{1}{3}\cdot {\left(-2\right)}^2=\frac{4}{3}.$

⦁ Với x = –1 thì $y=\frac{1}{3}\cdot {\left(-1\right)}^2=\frac{1}{3}.$

⦁ Với x = 0 thì $y=\frac{1}{3}\cdot 0^2=0.$

⦁ Với x = 1 thì $y=\frac{1}{3}\cdot 1^2=\frac{1}{3}.$

⦁ Với x = 2 thì $y=\frac{1}{3}\cdot 2^2=\frac{4}{3}.$

⦁ Với x = 3 thì $y=\frac{1}{3}\cdot 3^2=3.$

Ta có bảng sau:

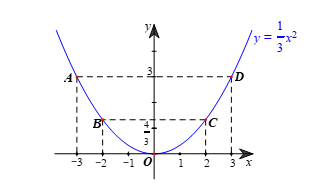
b) – Vẽ các điểm A(–3; 3); $B\left(–2;\frac{4}{3}\right);$ O(0; 0); $C\left(2;\frac{4}{3}\right);$ D(3; 3) thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ trong mặt phẳng tọa độ Oxy.

– Vẽ đường parabol đi qua 5 điểm A, B, O, C, D, ta nhận được đồ thị của hàm số $y=\frac{1}{3}{x}^2$ (hình vẽ).

c) ⦁ Điểm có hoành độ bằng –6 tức là x = –6.

Với x = –6, thay vào hàm số $y=\frac{1}{3}{x}^2,$ ta được $y=\frac{1}{3}\cdot {\left(-6\right)}^2=12.$

Suy ra điểm thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ có hoành độ bằng –6 thì có tọa độ (–6; 12).

⦁ Điểm có hoành độ bằng 10, tức là x = 10.

Với x = 10, thay vào hàm số $y=\frac{1}{3}{x}^2,$ ta được $y=\frac{1}{3}\cdot {10}^2=\frac{100}{3}.$

Suy ra điểm thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ có hoành độ bằng 10 thì có tọa độ $\left(10;\frac{100}{3}\right).$

d) Điểm có tung độ bằng 27, tức là y = 27.

Với y = 27, thay vào hàm số $y=\frac{1}{3}{x}^2,$ ta được:

81 = x², suy ra x = 9 hoặc x = –9.

Vậy những điểm thuộc đồ thị hàm số $y=\frac{1}{3}{x}^2$ có tung độ bằng 27 thì có tọa độ là (9; 27) và (–9; 27).

Lời giải bài tập Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) hay, chi tiết khác:

• Khởi động trang 46 Toán 9 Tập 2: Galileo Galilei (1564 – 1642), sinh tại thành phố Pisa (Italia), là nhà bác học vĩ đại của thời kì Phục Hưng.....

• Hoạt động 1 trang 46 Toán 9 Tập 2: Xét hàm số y = 5x² trong tình huống ở phần mở đầu.....

• Luyện tập 1 trang 47 Toán 9 Tập 2: Hàm số nào sau đây có dạng y = ax² (a ≠ 0)? Đối với những hàm số đó, xác định hệ số a của x².....

• Luyện tập 2 trang 47 Toán 9 Tập 2: Cho hàm số $y=\frac{2}{3}{x}^2.$ Tính giá trị của y khi:....

• Hoạt động 2 trang 47 Toán 9 Tập 2: a) Nêu khái niệm đồ thị của hàm số y = f(x). b) Xét hàm số y = 2x². Hãy thực hiện các hoạt động sau:....

• Luyện tập 3 trang 49 Toán 9 Tập 2: Vẽ đồ thị của hàm số y = –3x².....

• Hoạt động 3 trang 49 Toán 9 Tập 2: Quan sát đồ thị của hàm số $y=\frac{1}{2}{x}^2$ ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H; F và G đối với trục Oy.....

• Bài 1 trang 51 Toán 9 Tập 2: Cho hàm số y = ax². Tìm a, biết rằng khi x = –3 thì y = 5....

• Bài 3 trang 51 Toán 9 Tập 2: Trong mặt phẳng toạ độ Oxy, điểm M(2; –1) thuộc đồ thị của hàm số y = ax²...

• Bài 4 trang 51 Toán 9 Tập 2: Hàm số y = at² biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125 m....

• Bài 5 trang 51 Toán 9 Tập 2: Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol y = ax²....