Bài 5 trang 51 Toán 9 Tập 2 Cánh diều

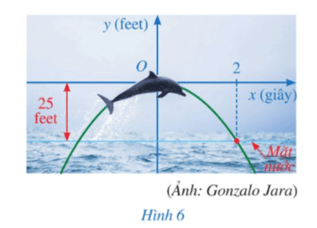
Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol y = ax, với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. Tìm hàm số biểu thị quỹ đạo nhảy của cá heo.

Giải Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) - Cánh diều

Bài 5 trang 51 Toán 9 Tập 2: Cá heo có thể nhảy cao tới 25 feet và thực hiện các thủ thuật như nhảy qua vòng, lộn nhào trong không trung. Giả sử quỹ đạo nhảy của cá heo là parabol y = ax², với gốc tọa độ là vị trí cao nhất mà cá heo đạt được, cách mặt nước 25 feet, trong đó y được tính theo đơn vị feet và x được tính theo đơn vị giây (Hình 6). Biết rằng sau 2 giây kể từ vị trí cao nhất đó, cá heo rơi chạm mặt nước. Tìm hàm số biểu thị quỹ đạo nhảy của cá heo.

Lời giải:

Vì quỹ đạo nhảy của cá heo là parabol y = ax², với gốc tọa độ là vị trí cao nhất mà cá heo đạt được nên đồ thị của hàm số y = ax² nằm bên dưới trục hoành.

Mà theo bài, sau 2 giây kể từ vị trí cao nhất cách mặt nước 25 feet, cá heo rơi chạm mặt nước nên ta có x = 2 và y = –25.

Thay x = 2 và y = –25 vào hàm số y = ax², ta được:

–25 = a.2² hay 4a = –25. Suy ra $a=–\frac{25}{4}.$

Vậy hàm số biểu thị quỹ đạo nhảy của cá heo là $y=-\frac{25}{4}{x}^2.$

Lời giải bài tập Toán 9 Bài 1: Hàm số y = ax^2 (a ≠ 0) hay, chi tiết khác:

• Khởi động trang 46 Toán 9 Tập 2: Galileo Galilei (1564 – 1642), sinh tại thành phố Pisa (Italia), là nhà bác học vĩ đại của thời kì Phục Hưng.....

• Hoạt động 1 trang 46 Toán 9 Tập 2: Xét hàm số y = 5x² trong tình huống ở phần mở đầu.....

• Luyện tập 1 trang 47 Toán 9 Tập 2: Hàm số nào sau đây có dạng y = ax² (a ≠ 0)? Đối với những hàm số đó, xác định hệ số a của x².....

• Luyện tập 2 trang 47 Toán 9 Tập 2: Cho hàm số $y=\frac{2}{3}{x}^2.$ Tính giá trị của y khi:....

• Hoạt động 2 trang 47 Toán 9 Tập 2: a) Nêu khái niệm đồ thị của hàm số y = f(x). b) Xét hàm số y = 2x². Hãy thực hiện các hoạt động sau:....

• Luyện tập 3 trang 49 Toán 9 Tập 2: Vẽ đồ thị của hàm số y = –3x².....

• Hoạt động 3 trang 49 Toán 9 Tập 2: Quan sát đồ thị của hàm số $y=\frac{1}{2}{x}^2$ ở Hình 4, hãy nêu nhận xét về vị trí cặp điểm E và H; F và G đối với trục Oy.....

• Bài 1 trang 51 Toán 9 Tập 2: Cho hàm số y = ax². Tìm a, biết rằng khi x = –3 thì y = 5....

• Bài 2 trang 51 Toán 9 Tập 2: Cho hàm số $y=\frac{1}{3}{x}^2.$a) Tìm giá trị của y tương ứng với giá trị của x trong bảng sau:...

• Bài 3 trang 51 Toán 9 Tập 2: Trong mặt phẳng toạ độ Oxy, điểm M(2; –1) thuộc đồ thị của hàm số y = ax²...

• Bài 4 trang 51 Toán 9 Tập 2: Hàm số y = at² biểu thị quãng đường (đơn vị: mét) mà một chiếc xe đua đi được trong khoảng thời gian t (giây). Giả sử một chiếc xe đua đi được 125 m....