Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho góc B = alpha
Câu hỏi:
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.
Trả lời:
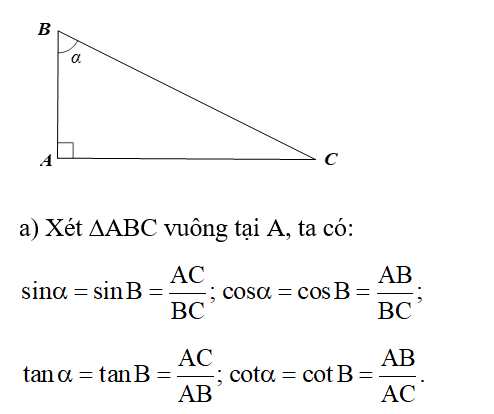
Câu hỏi:
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A sao cho
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.
Trả lời:

Câu 1:
Cho góc nhọn Xét tam giác ABC vuông tại A, tam giác A’BC’ vuông tại A’ với A, A’ thuộc tia Bx và C, C’ thuộc tia By (Hình 1). Do ∆ABC ᔕ ∆A’BC’ nên
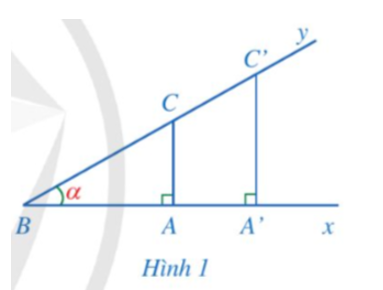
Như vậy, tỉ số giữa cạnh đối AC của góc nhọn α và cạnh huyền BC trong tam giác vuông ABC không phụ thuộc vào việc chọn tam giác vuông đó.
Tỉ số có mối liên hệ như thế nào với độ lớn góc α?
Câu 2:
Cho tam giác ABC vuông tại A có (Hình 2).
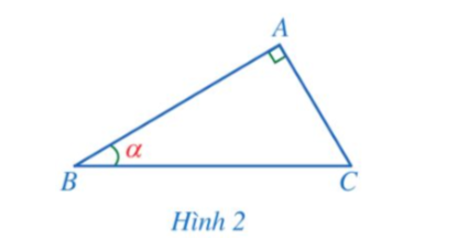
a) Cạnh góc vuông nào là cạnh đối của góc B?
Câu 5:
b) Chứng minh:
Từ đó, tính giá trị biểu thức: S = sin235° + cos235°; T = tan61°.cot61°.
Câu 6:
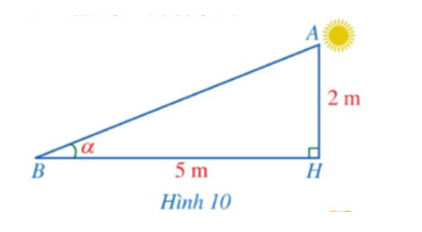
Hình 10 mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.